mary_britgit
New member
- Xu
- 0
Tìm x biết: \[|x|x^{2}+\frac{3}{4}||=x\]
Sửa lần cuối bởi điều hành viên:



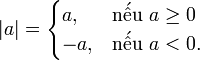

bên trái là trị tuyệt đối nên pt có nghiệm khi bên phải >=0Đối với giá trị tuyệt đối thì chia làm 2 trường hợp:
+Trường hợp 1:
x(x^2 +3/4)=x (Nếu x lớn hơn hoặc bằng 0)
<=>x^3 +(3/4)x =x
Chuyển vế, ta được:
<=>x^3 - (1/4)x =0
Đặt x làm nhân tử chung:
<=>x(x^2-1/4) =0(Ra phương trình tích)
Khi đó: x=0 hoặc x^2-1/4=0
x=0 hoặc x^2=1/4
x=0 hoặc x=căn bâc hai của 1/4 là 1/2(nhận) và -1/2(loại)
+Trường hợp 2:
x(x^2+3/4)=-x( Nếu x nhỏ hơn 0)
<=>x^3+(3/4)x=-x
<=>x^3+(7/4)x=0
<=>x(x^2+7/4)=0
Khi đó: x=0 hoặc x^2+7/4=0
x=0 hoặc x^2=-7/4(Vô lí vì bình phương của một số luôn không âm)
Kết luân: x=0 hoặc x=1/2
Phương pháp đặt nhân tử chung:
a^2+ab=a(a+b)
Cách giải phương trình tích:
Ví dụ: (a-b)(a+b)=0 thì em sẽ có:
a-b=0 hoặc a+b=0.
Vì cái này lên lớp 8 em mới học, nhưng anh chỉ cho em biết trước luôn. Chúc em học tốt.
