-
Chào mừng Bạn tham gia Diễn Đàn VNKienThuc.com - Định hướng Forum Kiến Thức - HÃY TẠO CHỦ ĐỀ KIẾN THỨC HỮU ÍCH VÀ CÙNG NHAU THẢO LUẬN Kết nối: VnKienthuc FB - VNK groups | Nhà Tài Trợ: Trúc Coffee - Mì Cay Hàn Quốc - Cafe & Trà chanh Bắc Ninh
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Toán 6 về chia hết
- Thread starter vovanninh
- Ngày gửi
pepj_ngok96
New member
- Xu
- 0
Bài 2: Tìm các số tự nhiêncó ba chữ số khác nhau sao cho 3a + 5b = 8c.
3a + 5b = 8c <=> 3a - 3c = 5c - 5b <=> 3(a-c) = 5(c-b) (1)
Có a#b#c; 3 và 5 là số nguyên tố cùng nhau.
Từ (1) ta có: (a-c) chia hết cho 5 và (c-b) chia hết cho 3. Ta thấy: -9 \[\leq \] a-c \[\leq \] 9
*) Nếu: a-c = -5 => pt (1) <=> c-b = -3 <=> c-a = 5 và b-c = 3
cộng từng vế với nhau ta được: b-a = 8 => a=1; b=9; c=4
=> ta được số: 194
*) Nếu: a-c = 5 => pt (1) <=> c-b = 3
cộng từng vế ta đc: a-b = 8 => a = 8 ; b=0 ; c=3 hoặc a=9; b=1; c=4
=> ta đc 2 số: 803 và 914
Từ (1) ta có: (a-c) chia hết cho 5 và (c-b) chia hết cho 3. Ta thấy: -9a-c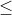 9
9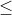
Đoạn: -9
Xếp Hạng
-
9,004
Butchi
-
5,099
Hide Nguyễn
-
4,373
ButNghien
-
4,161
Thandieu2
-
2,719
Trang Dimple
-
2,579
ngan trang
-
2,214
Văn Sử Địa
-
2,069
ButBi
-
1,891
Nguyễn Thành Sáng
-
1,766
h2y3
Tương tác
-
Hồ Chí Minh – Anh Hùng Giải Phóng Dân Tộc, Danh Nhân Văn Hóa Thế Giới
- Latest: Trang Dimple
-
Hồ Chí Minh – Hành Trình Cả Cuộc Đời Vì Độc Lập Và Tự Do Của Dân Tộc
- Latest: Trang Dimple
-
-
Ngoại Giao Vì Độc Lập: Hành Trình Tìm Đường Giải Phóng Dân Tộc Của Việt Nam
- Latest: Trang Dimple
-
Từ Đổi Mới Đến Phát Triển: Việt Nam Đã Thay Đổi Như Thế Nào Sau Năm 1986?
- Latest: Trang Dimple
Chủ đề mới
-
Thông Báo Điều hòa âm trần LG tự hào thương hiệu Hàn, Nhập khẩu Thái và Dịch vụ Thi công uy tín
- Started by vinhphat
- Trả lời: 0
-
-
Du Lịch Gắn Kết Gia Đình Qua Những Hành Trình Xuyên Lục Địa Liên Tuyến Mỹ
- Started by vietnhanco
- Trả lời: 0
-
Video YouTube ngâm bài Thơ Nhạc: Tiếng Tơ Lòng
- Started by Nguyễn Thành Sáng
- Trả lời: 0
-
Video YouTube ngâm bài Thơ Nhạc: Xin Hãy Cho Tôi
- Started by Nguyễn Thành Sáng
- Trả lời: 0
Dành cho học sinh
-
Hồ Chí Minh – Anh Hùng Giải Phóng Dân Tộc, Danh Nhân Văn Hóa Thế Giới
- Started by Trang Dimple
- Trả lời: 0
-
Hồ Chí Minh – Hành Trình Cả Cuộc Đời Vì Độc Lập Và Tự Do Của Dân Tộc
- Started by Trang Dimple
- Trả lời: 0
-
Từ Sau 1975 Đến Nay: Hành Trình Ngoại Giao Đưa Việt Nam Ra Thế Giới
- Started by Trang Dimple
- Trả lời: 0
-
Những Cuộc Đàm Phán Làm Thay Đổi Lịch Sử Việt Nam trong kháng chiến chống Pháp và kháng chiến chống Mỹ
- Started by Trang Dimple
- Trả lời: 0
-
Ngoại Giao Vì Độc Lập: Hành Trình Tìm Đường Giải Phóng Dân Tộc Của Việt Nam
- Started by Trang Dimple
- Trả lời: 0
-
Từ Đổi Mới Đến Phát Triển: Việt Nam Đã Thay Đổi Như Thế Nào Sau Năm 1986?
- Started by Trang Dimple
- Trả lời: 0
-
1986 – Bước Ngoặt Lịch Sử: Khi Việt Nam Bắt Đầu Công Cuộc Đổi Mới
- Started by Trang Dimple
- Trả lời: 0
-
Cuộc kháng chiến chống Mỹ, cứu nước (1954–1975)- 21 Năm Chiến Đấu: Làm Sao Việt Nam Có Thể Đánh Bại Siêu Cường Mỹ?
- Started by Trang Dimple
- Trả lời: 4
-
Cuộc kháng chiến chống thực dân Pháp (1945–1954)- Hành Trình 9 Năm Kháng Chiến Gian Khổ Nhưng Hào Hùng
- Started by Trang Dimple
- Trả lời: 0
Trending content
Định hướng
Diễn đàn VnKienthuc.com là nơi thảo luận và chia sẻ về mọi kiến thức hữu ích trong học tập và cuộc sống, khởi nghiệp, kinh doanh,...
