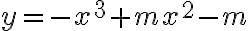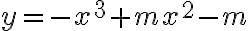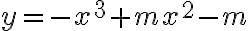các bác giúp em với
Hàm số
đồng biến trên (1;2) thì m thuộc khoảng nào
giải chi tiết được ạ
thanhs nhiều
xét \[y'=-3x^2+2mx\]
hàm số đồng biến trên khoảng (1;2) khi \[y'>0\] với mọi x thuộc khoảng trên. Bạn có thể làm theo cách định lượng toán học (công thức biến đổi) mình thử làm theo kiểu định tính các bạn xem có được không nha.
xét tiếp \[g(x)=-3x^2+2mx\] hàm số đạt max với \[x=\frac{m}{3}\]
nếu \[x=\frac{m}{3}\] không thuộc khoảng (1;2)
tức là \[x=\frac{m}{3}>2\] hoặc \[x=\frac{m}{3}<1\] nói cách khác m>6 hoặc m<3 thì điều kiện cần thiết là
\[y'(1)>0\] và \[y'(2)>0\]
(bạn tự giải rồi đối chiếu với điều kiện của trường hợp nhé)
còn ngược lại 3<m<6 thì ngoài điều kiện
\[y'(1)>0\] và \[y'(2)>0\] thì cần \[y'(\frac{m}{3}) \]
*đó là trên phương diện lý thuyết, còn y' đạt max tại \[x=\frac{m}{3}\] rồi thì không cần đk đó trong trường hợp này, nhưng với hệ số của \[x^2\] dương thì điều đó là bắt buộc*
kết quả thế nào chắc sau bài này bạn tìm được rồi!
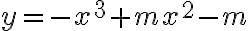 đồng biến trên (1;2) thì m thuộc khoảng nào
đồng biến trên (1;2) thì m thuộc khoảng nào