Toán 12 - Chương III - Bài 5. Ôn tập cuối năm
I - Bài tập tự luận
1. Cho hình lăng trụ ABC.A’B’C’ với cạnh bên không vuông góc với mặt đáy. Gọi
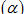
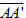
a) Chứng minh rằng thể tích V của hình lăng trụ đã cho bằng thể tích của hình lăng trụ PQR.P’Q’R’.
b) Chứng minh rằng V = S[SUB]PQR[/SUB].AA’, trong đó S[SUB]PQR[/SUB] là diện tích tam giác PQR.
2. Cho tứ diện ABCD có thể tích V. Hãy tính thể tích của hình tứ diện có đỉnh là trọng tâm các mặt của tứ diện đã cho.
3. Cho hình hộp ABCD.A’B’C’D’ có thể tích V. Hãy tính thể tích của hình tứ diện ACB’D’.
4. Chứng minh rằng trung điểm các cạnh của một hình tứ diện đều là các đỉnh của một hình tám mặt đều. Hãy so sánh thể tích của tứ diện đều đã cho và thể tích của hình tám mặt đều đó.
5. Cho hình vuông ABCD nội tiếp đường tròn (O ; R). Gọi H là hình gồm các điểm của hình tròn (O; R) nhưng không nằm trong hình vuông. Tính thể tích hình tròn xoay sinh bởi hình H khi quay quanh đường thẳng chứa một đường chéo của hình vuông.
6. Cho lục giác đều ABCDEF cạnh a.
a) Tính thể tích hình tròn xoay sinh bởi lục giác đó khi quay quanh đường thẳng AD.
b) Tính thể tích hình tròn xoay sinh bởi lục giác đó khi quay quanh đường thẳng đi qua trung điểm của các cạnh AB và DE.
7. Cho hình trụ có bán kính R và đường cao
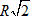
a) Chứng minh rằng ABCD là tứ diện đều.
b) Chứng minh rằng các đường thẳng AC, AD, BC, BD luôn tiếp xúc với một mặt trụ cố định (tức là khoảng cách giữa mỗi đường thẳng đó và trục của mặt trụ bằng bán kính mặt trụ).
8. Trong không gian tọa độ Oxyz, cho các điểm A(1; 5; 3), B(4; 2; -5), C(5; 5; -1) và D(1; 2; 4).
a) Chứng tỏ rằng bốn điểm A, B, C, D không đồng phẳng.
b) Viết phương trình mặt cầu (S) đi qua bốn điểm A, B, C, D. Xác định tâm và tính bán kính của mặt cầu đó.
c) Viết phương trình mặt phẳng đi qua ba điểm A, B, C và tìm khoảng cách từ điểm D tới mặt phẳng đó.
d) Viết phương trình mặt phẳng vuông góc với CD và tiếp xúc với mặt cầu (S).
e) Tìm bán kính các đường tròn giao tuyến của mặt cầu (S) và các mặt phẳng tọa độ.
9. Trong không gian tọa độ Oxyz, cho đường thẳng

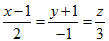
a) Viết phương trình hình chiếu của

b) Chứng minh rằng mặt phẳng x + 5y + z + 4 = 0 đi qua đường thẳng

c) Tính khoảng cách giữa đường thẳng

d) Viết phương trình đường vuông góc chung của hai đường thẳng


e) Viết phương trình đường thẳng song song với Oz, cắt cả


10. Trong không gian tọa độ Oxyz, cho hai điểm A(1; -1; 2), B(2; 0; 1) .
a) Tìm quỹ tích các điểm M sao cho MA[SUP]2[/SUP] - MB[SUP]2[/SUP] = 2.
b) Tìm quỹ tích các điểm N sao cho NA[SUP]2[/SUP] + NB[SUP]2[/SUP] = 3.
c) Tìm quỹ tích các điểm cách đều hai mặt phẳng (OAB) và (Oxy).
11. Trong không gian tọa độ Oxyz, cho đường thẳng

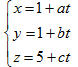
trong đó a, b, c thay đổi sao cho c[SUP]2[/SUP] = a[SUP]2[/SUP] + b[SUP]2[/SUP].
a) Chứng minh đường thẳng


b) Tìm quỹ tích giao điểm của

12. Cho hình hộp chữ nhật ABCD.A’B’C’D’ với AB = a, BC = b, CC’ = c.
a) Tính khoảng cách từ điểm A tới mp(A’BD).
b) Tính khoảng cách từ điểm A’ tới đường thẳng C’D.
c) Tính khoảng cách giữa hai đường thẳng BC’ và CD’.
II - Câu hỏi trắc nghiệm
1. Cho H là hình chóp tứ giác đều S.ABCD. Xét các mặt phẳng: (SAC), (SAB), (SBD), (ABC), (SOI), trong đó I là trung điểm của AB, O là tâm hình vuông ABCD. Trong các mặt phẳng đó, có bao nhiêu mặt phẳng là mặt phẳng đối xứng của H ?
A. 1
B. 2
C. 3
D. 4
2. Gọi H là lăng trụ lục giác đều ABCDEF.A’B’C’D’E’F’. Xét các mặt phẳng: mp(AA’D), mp(ACA’), mp(ABB’), mặt phẳng trung trực của DD’, mặt phẳng trung trực của AB. Trong các mặt phẳng đó, có bao nhiêu mặt phẳng là mặt phẳng đối xứng của H ?
A. 1
B. 2
C. 3
D. 4
3. Cho khối lăng trụ tam giác ABC.A’B’C’, M là trung điểm của cạnh AB. Trong các đẳng thức sau đây, đẳng thức nào sai ?
A. V[SUB]A’B’C’C[/SUB] = V[SUB]MA’B’C’[/SUB]
B. V[SUB]ABCC’[/SUB] = V[SUB]A’BCC’[/SUB]
C. V[SUB]MA’B’C’[/SUB] = V[SUB]A’ABC[/SUB]
D. V[SUB]MA’B’C’[/SUB] = 1/2V[SUB]AA’B’C’[/SUB]
4. Cho khối lăng trụ tam giác ABC.A’B’C’. Trong các đẳng thức sau đây, đẳng thức nào sai ?
A. V[SUB]A’B’CC’[/SUB] = 1/3V[SUB]ABC.A’B’C’[/SUB]
B. V[SUB]A.BB’C’C[/SUB] = 1/2V[SUB]ABC.A’B’C’[/SUB]
C. V[SUB]A.BCC’B’ [/SUB]= 2V[SUB]AA’BC[/SUB]
5. Cho khối chóp tứ giác S.ABCD và các điểm A’, B’, C’, D’ lần lượt nằm trên các đường thẳng SA, SB, SC, SD nhưng không trùng với S.
Trong các mệnh đề sau đây, mệnh đề nào đúng?

6. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Hình lăng trụ nội tiếp một mặt cầu nếu đáy của nó là đa giác nội tiếp;
B. Hình lăng trụ nội tiếp một mặt cầu nếu tất cả các mặt của nó đều là đa giác nội tiếp;
C. Hình lăng trụ nội tiếp một mặt cầu nếu có mặt bên vuông góc với mặt đáy;
D. Đa diện nội tiếp một mặt cầu nếu các mặt của nó đều là đa giác nội tiếp.
7. Trong các mệnh đề sau, mệnh đề nào đúng?
A. Đường tròn đi qua ba điểm phân biệt nằm trên mặt cầu thì nằm hoàn toàn trên mặt cầu;
B. Có duy nhất một mặt cầu đi qua 4 đỉnh của một hình thang cân cho trước;
C. Hình chóp có đáy là hình thang vuông luôn luôn nội tiếp một mặt cầu;
D. Cả ba mệnh đề trên đều sai.
8. Cho khối trụ có bán kính
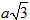
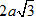

9. Đáy của một hình chóp là hình vuông có diện tích bằng 4. Các mặt bên của nó là những tam giác đều. Diện tích toàn phần của hình chóp là

10. Một hình nón có đường sinh bằng l và bằng đường kính đáy. Bán kính hình cầu nội tiếp hình nón là

11. Một hình cầu có thể tích bằng 4
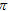
A. 8
B.
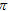
C. 1
D.
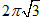
12. Cho hình chữ nhật có hai đỉnh A(-2; 3; 0) , B(2; 3; 0) và một cạnh nằm trên Ox. Khối tròn xoay sinh bởi hình chữ nhật đó khi quay quanh trục Oy có thể tích là
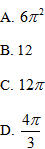
13. Cho hai vectơ
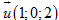
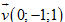
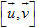

14. Cho tam giác ABC có diện tích bằng 6 nằm trong mặt phẳng
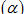
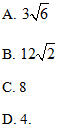
15. Mặt cầu tâm I(6; 3; -4), tiếp xúc với trục Ox có bán kính là
A. 5
B.
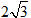
C.
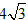
D. 4
16. Cho đường thẳng d có phương trình:
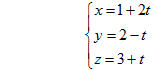
Phương trình tham số nào sau đây cũng là phương trình của d ?
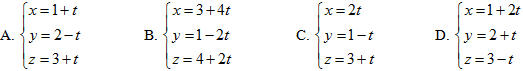
17. Cho hai đường thẳng
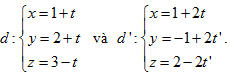
Khi đó:
A. d cắt d’ ;
B. d trùng d’ ;
C. d và d’ chéo nhau ;
D. d song song với d’ .
18. Cho mặt phẳng (P) và mặt cầu (S) có phương trình
(P): 3x + 4z + 12 = 0 ;
(S): x[SUP]2[/SUP] + y[SUP]2[/SUP] + (z - 2)[SUP]2[/SUP] = 1
Khi đó:
A. mp(P) đi qua tâm mặt cầu (S) ;
B. mp(P) tiếp xúc với mặt cầu (S) ;
C. mp(P) cắt (S) theo một đường tròn ;
D. mp(P) không cắt (S).
19. Tọa độ hình chiếu vuông góc của điểm M(2; 0; 1) trên đường thẳng
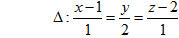
A. (1; 0; 2)
B. (2; 2; 3)
C. (0; -2; 1)
D. (-1; 4; 0)
20. Cho hai đường thẳng
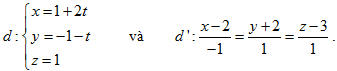
Khoảng cách giữa d và d’ là

21. Cho hai đường thẳng
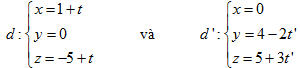
Phương trình đường vuông góc chung của d và d’ là

22. Cho mặt phẳng (P): mx + y + (n - 2)z + m + 2 = 0. Với mọi m, n, mặt phẳng (P) luôn đi qua điểm cố định có tọa độ là
A. (1; 2; 0)
B. (2; 1; 0)
C. (0; 1; -2)
D. (-1; -2; 0)
23. Cho mặt cầu (S): x[SUP]2[/SUP] + y[SUP]2[/SUP] + z[SUP]2[/SUP] - 2x -4y -4z = 0. Mặt phẳng tiếp xúc với (S) tại điểm A(3; 4; 3) có phương trình:
A. 4x + 4y - 2z - 17 = 0
B. 2x + 2y + z - 17 = 0
C. 2x + 4y + z - 17 = 0
D. x + y + z - 17 = 0
III - Một số đề kiểm tra
ĐỀ I
Câu 1. Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và cạnh bên bằng
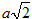
a) Tính thể tích của hình chóp đã cho.
b) Tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD.
c) Gọi A’ và C’ lần lượt là trung điểm của hai cạnh SA và SC. Chứng minh rằng hai hình chóp A’.ABCD và C’.CBAD bằng nhau.
Câu 2. Trong không gian tọa độ Oxyz, cho các điểm A(4; -1; 2), B(1; 2; 2) và C(1; -1; 5).
a) Chứng minh rằng ABC là tam giác đều.
b) Viết phương trình mp(ABC). Tính thể tích khối tứ diện giới hạn bởi mp(ABC) và các mặt phẳng tọa độ.
c) Viết phương trình trục của đường tròn ngoại tiếp tam giác ABC.
d) Tìm tọa độ điểm D sao cho ABCD là tứ diện đều.
ĐỀ II
Câu 1. Cho tứ diện đều ABCD có cạnh bằng a. Gọi B’, C’, D’ lần lượt là trung điểm của các cạnh AB, AC và AD.
a) Chứng minh rằng sáu điểm B, C, D, B’, C’, D’ nằm trên một mặt cầu. Tính bán kính của mặt cầu đó.
b) Tính thể tích khối chóp D.BCC’B’.
Câu 2. Trong không gian tọa độ Oxyz, cho các điểm A(2; 0; 0 ), A’(6; 0; 0) , B(0; 3; 0), B’(0; 4; 0), C(0; 0; 4), C’(0; 0; 3).
a) Viết phương trình mặt cầu đi qua bốn điểm A, A’, B, C. Chứng minh rằng B’ và C’ cũng nằm trên mặt cầu đó.
b) Chứng minh rằng trực tâm H của tam giác ABC, trọng tâm G của tam giác A’B’C’ cùng nằm trên một đường thẳng đi qua O. Viết phương trình đường thẳng đó.
c) Tính khoảng cách từ điểm O tới giao tuyến của mp(ABC’) và mp(A’B’C).
ĐỀ III
Câu 1. Cho hình hộp ABCD.A’B’C’D’. Gọi N là điểm nằm trên cạnh AB và
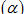
a) Mặt phẳng
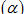
b) Chứng minh rằng mặt phẳng
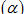
c) Tính tỉ số thể tích của khối đa diện H[SUB]1[/SUB] và thể tích của khối tứ diện AA’BD.
Câu 2. Trong không gian tọa độ Oxyz, cho các điểm A(1; -3; -1) và B(-2; 1; 3).
a) Chứng tỏ rằng hai điểm A và B cách đều trục Ox.
b) Tìm điểm C nằm trên trục Oz sao cho tam giác ABC vuông tại C.
c) Viết phương trình hình chiếu của đường thẳng AB trên mp(Oyz).
d) Viết phương trình mặt cầu đi qua ba điểm O, A, B và có tâm nằm trên mp(Oxy).
SƯU TẦM
