Toán 12- Nâng Cao - Chương I - Bài 5. ÔN TẬP CHƯƠNG I
ÔN TẬP CHƯƠNG I
I - Kiến thức cần nhớ
1. Hình đa diện gồm một số hữu hạn đa giác phẳng thỏa mãn hai điều kiện :
a) Hai đa giác bất kì hoặc không có điểm chung, hoặc có một đỉnh chung, hoặc có một cạnh chung.
b) Mỗi cạnh của một đa giác là cạnh chung của đúng hai đa giác.
Hình đa diện chia không gian thành hai phần (phần bên trong và phần bên ngoài). Hình đa diện cùng với phần bên trong của nó gọi là khối đa diện.
2. Mỗi khối đa diện có thể phân chia được thành những khối tứ diện.
3. • Phép dời hình trong không gian là phép biến hình bảo toàn khoảng cách giữa hai điểm bất kì.
• Phép đối xứng qua mặt phẳng (P) là phép biến hình biến mỗi điểm thuộc (P) thành chính nó và biến mỗi điểm M không thuộc (P) thành điểm M[SUP]’[/SUP] sao cho (P) là mặt phẳng trung trực của đoạn thẳng MM[SUP]’[/SUP]. Phép đối xứng qua mặt phẳng là một phép dời hình.
• Mặt phẳng (P) gọi là mặt phẳng đối xứng của một khối đa diện nếu phép đối xứng qua (P) biến khối đa diện thành chính nó.
• Phép tịnh tiến, phép đối xứng trục, phép đối xứng tâm là những phép dời hình.
• Hai hình đa diện gọi là bằng nhau nếu có một phép dời hình biến hình này thành hình kia.
• Hai hình tứ diện bằng nhau nếu chúng có các cạnh tương ứng bằng nhau.
4. • Phép vị tự tâm O tỉ số k ≠ 0 là phép biến hình biến mỗi điểm M thành điểm M[SUP]’[/SUP] sao cho
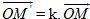
• Hình
5. Cho năm loại khối đa diện đều : khối tứ diện đều, khối lập phương, khối tám mặt đều, khối mười hai mặt đều, khối hai mươi mặt đều.
6. Thể tích của khối hộp chữ nhật bằng tích số ba kích thước.
7. Thể tích khối chóp bằng một phần ba tích số của diện tích mặt đáy và chiều cao của khối chóp.
8. Thể tích của khối lăng trụ bằng tích số của diện tích mặt đáy và chiều cao của khối lăng trụ.
II – Câu hỏi tự kiểm tra
1. Khối lăng trụ n-giác có bao nhiêu đỉnh, bao nhiêu cạnh và bao nhiêu mặt ?
Khối chóp n-giác có bao nhiêu đỉnh, bao nhiêu cạnh và bao nhiêu mặt ?
2. Những khối đa diện đều nào có mặt là tam giác đều ? Mỗi đỉnh của nó là đỉnh chung của bao nhiêu mặt ?
3. Nếu biết thể tích của một khối chóp và diện tích mặt đáy của nó thì có thể biết được chiều cao của khối chóp đó hay không ?
4. Nếu mỗi kích thước của một khối hộp chữ nhật đươc tăng lên k lần thì thể tích của khối chóp đó tăng lên bao nhiêu lần ?
5. Hình tứ diện đều, hình lập phương, hình bát diện đều có những mặt phẳng đối xứng nào ?
6. Nếu tỉ số các cạnh tương ứng của hai tứ diện đồng dạng bằng k thì tỉ số thể tích của hai khối tứ diện ấy bằng bao nhiêu ?
III – Bài tập
1. Cho tứ diện ABCD có thể tích bằng V. Gọi B[SUP]’[/SUP] và D[SUP]’[/SUP] lần lượt là trung điểm của AB và AD. Mặt phẳng (CB[SUP]’[/SUP]D[SUP]’[/SUP]) chia khối tứ diện thành hai phần. Tính thể tích mỗi phần đó.
2. Cho khối hộp ABCD.A[SUP]’[/SUP]B[SUP]’[/SUP]C[SUP]’[/SUP]D[SUP]’[/SUP]. Chứng minh rằng sáu trung điểm của sáu cạnh AB, BC, CC[SUP]’[/SUP], C[SUP]’[/SUP]D[SUP]’[/SUP], D[SUP]’[/SUP]A[SUP]’[/SUP] và A[SUP]’[/SUP]A nằm trên một mặt phẳng và mặt phẳng đó chia khối hộp thành hai phần có thể tích bằng nhau.
3. Cho khối tứ diện ABCD, E và F lần lượt là trung điểm của hai cạnh AB và CD. Hai mặt phẳng (ABF) và (CDE) chia khối tứ diện ABCD thành bốn khối tứ diện.
a) Kể tên bốn khối tứ diện đó.
b) Chứng tỏ rằng bốn khối tứ diện đó có thể tích bằng nhau.
c) Chứng tỏ rằng nếu ABCD là khối tứ diện đều thì bốn khối tứ diện nói trên bằng nhau.
4. Cho khối lăng trụ đứng ABC.A[SUP]’[/SUP]B[SUP]’[/SUP]C[SUP]’[/SUP] có diện tích đáy bằng S và AA[SUP]’[/SUP] = h. Một mặt phẳng (P) cắt các cạnh AA[SUP]’[/SUP], BB[SUP]’[/SUP], CC[SUP]’[/SUP] lần lượt tại A[SUB]1[/SUB], B[SUB]1[/SUB], vàC[SUB]1[/SUB]. Biết AA[SUB]1 [/SUB]= a, BB[SUB]1[/SUB] = b, CC[SUB]1[/SUB] = c.
a) Tính thể tích hai phần của khối lăng trụ được phân chia bởi mặt phẳng (P).
b) Với điều kiện nào của a, b, c thể tích của hai phần đó bằng nhau.
5. Cho khối lăng trụ đều ABC.A[SUP]’[/SUP]B[SUP]’[/SUP]C[SUP]’[/SUP] và M là trung điểm của cạnh AB. Mặt phẳng (B[SUP]’[/SUP]C[SUP]’[/SUP]M)chia khối lăng trụ thành hai phần. Tính tỉ số thể tích hai phần đó.
6. Cho khối chóp S.ABC có đường cao SA bằng a, đáy là tam giác vuông cân có AB = BC = a. Gọi B[SUP]’[/SUP] là trung điểm của SB, C[SUP]’[/SUP] là chân đường cao hạ từ A của tam giác SAC.
a) Tính thể tích của khối chóp S.ABC.
b) Chứng minh rằng SC vuông góc với mp (AB[SUP]’[/SUP]C[SUP]’[/SUP])
c) Tính thể tích khối chóp S.AB[SUP]’[/SUP]C[SUP]’[/SUP].
IV – Câu hỏi trắc nghiệm
1. Mỗi đỉnh của hình đa diện là đỉnh chung của ít nhất
(A) Năm cạnh ;(B) Bốn cạnh ;
(C) Ba cạnh ;(D) Hai cạnh .
2. Cho khối chóp có đáy là n-giác. Trong các mệnh đề sau đây, mệnh đề nào đúng ?
(A) Số cạnh của khối chóp bằng n + 1 ;
(B) Số mặt của khối chóp bằng 2n ;
(C) Số đỉnh của khố chóp bằng 2n + 1 ;
(D) Số mặt của khối chóp bằng số đỉnh của nó.
3. Phép đối xứng qua mp(P) biến đường thẳng d thành chính nó khi và chỉ khi
(A) d song song với (P) ;(B) d nằm trên(P) ;
(C) d ⊥ (P) ;(D) d nằm trên (P) hoặc d ⊥ (P) .
4. Cho hai đường thẳng d và d[SUP]’[/SUP] cắt nhau. Có bao nhiêu phép đối xứng qua mặt phẳng biến d thành d[SUP]’[/SUP] ?
(A) Có một ;(B) Có hai ;
(C) Không có ;(D) Có vô số.
5. Cho hai đường thẳng phân biệt d và d[SUP]’[/SUP] đồng phẳng. Có bao nhiêu phép đối xứng qua mặt phẳng biến d thành d[SUP]’[/SUP] ?
(A) Không có ;(B) Có một ;
(C) Có hai ;(D) Có một hoặc hai.
6. Hình chóp tứ giác đều có bao nhiêu mặt phẳng đối xứng ?
(A) Một ; (B) Hai ;
(C) Ba ;(D) Bốn.
7. Một hình hộp đứng có đáy hình thoi (không phải hình vuông) có bao nhiêu mặt phẳng đối xứng ?
(A) Một ; (B) Hai ;
(C) Ba ;(D) Bốn.
8. Cho phép vị tự tâm O biến điểm A thành điểm B, biết rằng OA = 2OB. Khi đó, tỉ số vị tự là bao nhiêu ?
(A) 2 ;(B) – 2 ;
(C)±
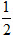
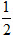
9. Cho hai đường thẳng song song d, d[SUP]’[/SUP] và một điểm O không nằm trên chúng. Có bao nhiêu phép vị tự tâm O biến d thành d[SUP]’[/SUP] ?
(A) Có một ; (B) Không có ;
(C) Có hai ;(D) Có một hoặc không có.
10. Khối tám mặt đều thuộc loại
(A) {3 ; 3} ; (B) {4 ; 3};
(C) {5 ; 3} ;(D) {3 ; 4}.
11. Khối hai mươi mặt đều thuộc loại
(A) {3 ; 4} ; (B) {3 ; 5};
(C) {4 ; 3} ;(D) {4 ; 5}.
12. Nếu ba kích thước của một khối hộp chữ nhật tăng lên k lần thì thể tích của nó tăng lên
(A) k lần ; (B) k[SUP]2[/SUP] lần ;
(C) k[SUP]3[/SUP] lần ; (D) 3k[SUP]3[/SUP] lần.
13. Tổng diện tích các mặt phẳng của một hình lập phương bằng 96. Thể tích của khối lập phương đó là
(A) 64 ; (B) 91 ;
(C) 84 ;(D) 48.
14. Ba kích thước của một hình hộp chữ nhật làm thành một cấp số nhân có công bội là 2. Thể tích hình hộp đã cho là 1728. Khi đó, các kích thước của hình hộp là
(A) 8, 16, 32 ; (B) 2, 4, 8 ;
(C) 2
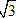
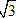
15. Các đường chéo của các mặt phẳng của một hình hộp chữ nhật bằng
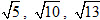
(A) 4 ; (B) 5 ;
(C) 6;(D) 8.
16. Một khối lăng trụ đứng tam giác có cạnh đáy bằng 37, 13, 30 và diện tích xung quanh bằng 480. Khi đó thể tích của khối lăng trụ là
(A) 2010 ; (B) 1010 ;
(C) 1080;(D) 2040.
17. Một khối lăng trụ tam giác có các cạnh đáy bằng 13, 14, 15, cạnh bên tạo với mặt phẳng đáy một góc 30[SUP]o[/SUP] và có chiều dài bằng 8. Khi đó thể tích của khối lăng trụ là
(A) 340 ; (B) 336 ;
(C) 274
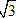
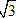
18. Đáy của một hình hộp đứng là hình thoi cạnh a, góc nhọn 60[SUP]o[/SUP]. Đường chéo lớn của đáy bằng đường chéo nhỏ của hình hộp. Khi đó thể tích của hình hộp là
(A) a[SUP]3[/SUP] ; (B) a[SUP]3[/SUP]
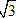
(C)
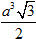
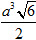
19. Khi độ dài cạnh của hình lập phương tăng thêm 2cm thì thể tích của nó tăng thêm 98cm[SUP]3[/SUP]. Cạnh của hình lập phương đã cho là
(A) 4cm ; (B) 5cm ;
(C) 6cm ;(D) 3cm.
20. Khi một hình hộp với sáu mặt đều là hình thoi cạnh a, góc nhọn bằng 60[SUP]o[/SUP]. Khi đó thể tích của hình hộp là
(A)
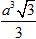
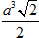
(C)
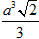
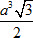
21. Cho một hình lập phương có cạnh bằng a. Khi đó, thể tích của khối tám mặt đều mà các đỉnh là tâm của các mặt của hình lập phương đã cho bằng

22. Cho một khối tứ diện đều có cạnh bằng a. Khi đó thể tích của khối tám mặt đều mà các đỉnh là trung điểm của các cạnh của khối tứ diện đã cho là

23. Cho khối mười hai mặt đều
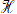
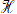

24. Một khối lăng trụ tam giác có các cạnh đáy bằng 19, 20, 37, chiều cao của khối lăng trụ bằng trung bình cộng của các cạnh đáy. Khi đó thể tích của khối lăng trụ là
(A) 2888 ; (B) 1245
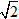
(C) 1123 ;(D) 4273.
25. Đáy của một hình hộp là một hình thoi cạnh bằng 6cm và góc nhọn bằng 45[SUP]o[/SUP], cạnh bên của hình hộp dài 10cm và tạo với mặt phẳng đáy một góc 45[SUP]o[/SUP]. Khi đó thể tích hình hộp là
(A) 124
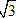
(C) 120
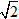
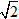
26. Với một tấm bìa hình vuông, người ta cắt bỏ ở mỗi góc tấm bìa một hình vuông cạnh 12cm rồi gấp lại thành một hình hộp chữ nhật không có nắp. Nếu dung tích của cái hộp đó là 4800cm[SUP]3[/SUP] thì cạnh tấm bìa có độ dài là
(A) 42cm ; (B) 36cm ;
(C) 44cm ;(D) 38cm.
27. Cho một hình chóp tam giác đều có cạnh đáy bằng a và cạnh bên tạo với mặt phẳng đáy một góc

28. Một hình chóp tam giác đều có cạnh bên bằng b và cạnh bên tạo với mặt phẳng đáy một góc

29. Cho hình tứ giác đều
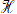
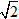
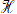

30. Một khối chóp tam giác có các cạnh đáy bằng 6, 8, 10. Một cạnh bên có độ dài bằng 4 và tạo với đáy góc 60[SUP]o[/SUP]. Thể tích của khối chóp đó là

31. Nếu một hình chóp đều có chiều cao và cạnh đáy cùng tăng lên n lần thì thể tích của nó tăng lên
(A) n[SUP]2[/SUP] lần ; (B) 2n[SUP]2[/SUP] lần ;
(C) n[SUP]3[/SUP] lần ;(D) 2n[SUP]3[/SUP] lần.
32. Khi chiều cao một hình chóp đều tăng lên n lần nhưng mỗi cạnh đáy giảm đi n lần thì thể tích của nó
(A) Không thay đổi ; (B) Tăng lên nlần ;
(C) Tăng lên (n - 1) lần ;(D) Giảm đi nlần.
SƯU TẦM
