Toán 12- Nâng Cao - Chương II - Bài 1. MẶT CẦU, KHỐI CẦU
CHƯƠNG II. MẶT CẦU, MẶT TRỤ, MẶT NÓN
Trong đời sống hằng ngày, chúng ta thường gặp những đồ vật có dạng hình cầu, hình trụ hoặc hình nón. Học xong chương này, học sinh cần hình dung được thế nào là mặt cầu, mặt trụ, mặt nón và những hình có quan hệ đến những mặt đó. Học sinh cần nhớ các công thức về diện tích và thể tích của hình cầu, hình trụ và hình nón.
§1 MẶT CẦU, KHỐI CẦU
1. Định nghĩa mặt cầu

Các quả bóng như bóng bàn, bóng đá, bóng chuyền cho ta hình ảnh của một hình trong không gian mà ta sẽ gọi là mặt cầu. Định nghĩa của mặt cầu cũng đơn giản như định nghĩa quen thuộc của đường tròn trong hình học phẳng.
ĐỊNH NGHĨA
Tập hợp các điểm trong không gian cách điểm O cố định một khoảng R không đổi gọi là mặt cầu có tâm O và bán khính bằng R.
Mặt cầu như thế thường được kí hiệu là S(O ; R). Như vậy :
S(O ; R) ={M | OM = R}.
Các thuật ngữ
Cho mặt cầu S(O ; R) và một điểm A nào đó (h.32).
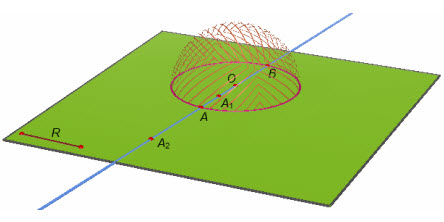
Hình 32
a) Nếu OA = R thì theo định nghĩa, điểm A thuộc mặt cầu. Khi đó đoạn thẳng OA cũng được gọi là bán kính của mặt cầu.
Nếu OA và OB là hai bán kính sao cho O, A, B thẳng hàng thì đoạn thẳng AB được gọi là đường kính của mặt cầu. Như vậy, một mặt cầu được xác định khi biết tâm và bán kính R hoặc khi biết một đường kính AB của nó.
b) Nếu OA < R thì ta nói rằng điểm A nằm trong mặt cầu.
c) Nếu OA > R thì ta nói rằng điểm A nằm ngoàimặt cầu.
Trên hình 32, ta có điểm A nằm trên mặt cầu, AB là đường kính, điểm A[SUB]1[/SUB] nằm trong mặt cầu và điểm A[SUB]2[/SUB] nằm ngoài mặt cầu.
d) Tập hợp các điểm thuộc mặt cầu S(O ; R) cùng với các điểm nằm trong mặt cầu đó được gọi là khối cầu S(O ; R) hoặc hình cầu S(O ; R). Như vậy, khối cầu S(O ; R) là tập hợp các điểm M sao cho OM ≤ R.
Một số ví dụ
Ví dụ 1. Cho hai điểm A, B cố định. Chứng minh rằng tập hợp các điểm M sao cho
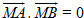
Giải. Gọi I là trung điểm của AB, ta có
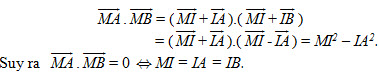
Vậy tập hợp các điểm M là mặt cầu tâm I bán kính R = IA, tức là mặt cầu đường kính AB. ¢
Ví dụ 2. Cho tứ diện đều ABCD có cạnh bằng a. Tìm tập hợp các điểm M sao cho
MA[SUP]2[/SUP] + MB[SUP]2[/SUP] + MC[SUP]2[/SUP] + MD[SUP]2[/SUP] = 2a[SUP]2[/SUP].

Gọi G là trọng tâm của tứ diện ABCD, ta có
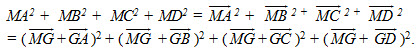
a) Hãy tính toán tiếp để đi đến kết quả :
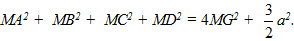
b) Hãy kết hợp kết quả trên với đẳng thức đã cho trong bài toán để tìm giá trị của MG.
c) Phát biểu kết quả của bài toán.
2. Vị trí tương đối giữa mặt cầu và mặt phẳng
Cho mặt phẳng S(O ; R) và mặt phẳng (P). Hiển nhiên mặt phẳng có thể cắt và không cắt mặt cầu. Nếu mặt cầu ở cách mặt phẳng quá xa thì rõ ràng là chúng không cắt nhau. Độ xa, gần của mặt cầu và mặt phẳng phụ thuộc vào bán kính R của mặt cầu và khoảng cách d từ tâmO của mặt cầu tới mặt phẳng (P). Gọi H là hình chiếu của O trên mp(P) thì d = OH.

Hãy chứng tỏ rằng điểm M là điểm chung của mặt cầu S(O ; R) và mp(P) khi và chỉ khi M ∈(P) và HM[SUP]2[/SUP] = R[SUP]2[/SUP] – d[SUP]2[/SUP] (h.33a).

Từ hoạt động 2, có thể luận gì về giao của hai mặt cầu S(O ; R) và (P) trong các trường hợp :
a) d < R ;
b) d = R ;
c) d > R ?
Tóm lại, ta có kết luận :
Cho mặt cầu S(O ; R) và mặt phẳng (P), gọi d là khoảng cách từ O tới (P) và H là hình chiếu của O trên (P). Khi đó :
• Nếu d theo giao tuyến là đường tròn nằm trên mặtphẳng (P) có tâm H và có bán kính
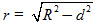
• Nếu d=R thì mp(P) cắt mặt cầu tại một điểm duy nhất H (h.33b).
• Nếu d>R thì mp(P) không cắt mặt cầu S(O ; R) (h.33c).
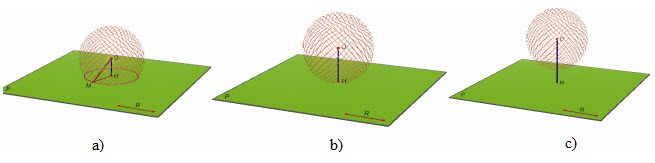
Hình 33
Khi d = 0 thì mp(P) đi qua tâm O của mặt cầu, mặt phẳng đó được gọi là mặt phẳng kính ; giao tuyến của mặt phẳng kính với mặt cầu là đường tròn có bán kính R, đường tròn đó gọi là đường tròn lớn của mặt cầu.
Trong trường hợp d=R, mp(P) và mặt cầu S(O ; R) có điểm chung duy nhất là H. Khi đó ta nói mặt phẳng (P) tiếp xúc với mặt cầu tại điểmH, hoặc còn nói mp(P) là tiếp diện của mặt cầu tại điểm H. Điểm H gọi là điểm tiếp xúc (hoặc tiếp điểm) của (P) và mặt cầu.
?1 Mệnh đề sau đây có đúng không : Điều kiện cần và đủ để mp(P) tiếp xúc với mặt cầu S(O ; R) tại điểm H là mp(P) vuông góc với bán kính OH tại điểm H ?
Bài toán 1
Mặt cầu đi qua mọi đỉnh của hình đa diện
Chứng minh rằng hình chóp nội tiếp một mặt cầu khi và chỉ khi đáy của nó là đa giác nội tiếp một đường tròn.

a) Nếu hình chóp S.A[SUB]1[/SUB]A[SUB]2[/SUB]…A[SUB]n[/SUB] nội tiếp một mặt cầu thì vì sao có thể kết luận rằng đa giác đáy A[SUB]1[/SUB]A[SUB]2[/SUB]…A[SUB]n[/SUB] nội tiếp một đường tròn ? Đó là đường tròn nào ?
b) Cho hình chóp đa giác đáy A[SUB]1[/SUB]A[SUB]2[/SUB]…A[SUB]n[/SUB] nội tiếp đường tròn tâm I. Hãy xác định điểm O cách đều tất cả các đỉnh của hình chóp. Từ đó suy ra hình chóp nội tiếp một mặt cầu.
?2 Tại sao có thể nói : Hình tứ diện nào cũng có mặt cầu ngoại tiếp ?
?3 Hình lăng trụ tam giác có cạnh bên không vuông góc với đáy có thể nội tiếp một mặt cầu không ? Vì sao ?
3. Vị trí tương đối giữa mặt cầu và đường thẳng
Cho mặt cầu S(O ; R) và đường thẳng ∆. Gọi H là hình chiếu của O trên ∆ và d = OH là khoảng cách từ O tới ∆. Hoàn toàn tương tự như trong trường hợp mặt cầu và mặt phẳng, ta có các kết luận sau đây (h.34) :
• Nếu d < R thì ∆ cắt mặt cầu tại hai điểm phân biệt (h.34a) ;
• Nếu d=R thì ∆ cắt mặt cầu tại một điểm phân biệt (h.34b) ;
• Nếu d>R thì ∆ không cắt mặt cầu (h.34c) ;
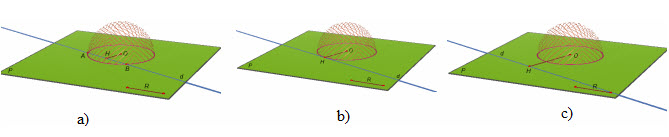
Hình 34
Trong trường hợp d=R , đường thẳng ∆ và mặt cầu S(O ; R) có điểm chung duy nhất là H. Khi đó, ta nói đường thẳng ∆ tiếp xúc với mặt cầu tại điểm H hoặc còn nói ∆ là tiếp tuyến của mặt cầu tại H. Điểm H gọi là điểm tiếp xúc (hoặc tiếp điểm) của ∆ và mặt cầu.
?4 Trong các mệnh đề sau đây, mệnh đề nào đúng ?
a) Điều kiện cần và đủ để đường thẳng ∆ tiếp xúc với mặt cầu S(O ; R) tại điểm H là ∆ vuông góc với bán kính OH tại điểm H ;
b) Có vô số đường thẳng tiếp xúc với mặt cầu S(O ; R) tại điểm H, chúng nằm trên mặt phẳng tiếp xúc với mặt cầu tại H.
Bài toán 2. Hãy chứng minh rằng có một mặt cầu tiếp xúc với các cạnh của một tứ diện đều ABCD cho trước.

Gọi O là trọng tâm của tứ diện đều ABCD. Hãy chứng minh rằng khoảng cách từ O tới các cạnh của tứ diện đó đều bằng nhau.
?6 Đường thẳng đi qua điểm A nằm trong mặt cầu có tiếp xúc với mặt cầu hay không ?
Trong trường hợp điểm A nằm ngoài mặt cầu, ta có định lí sau :
ĐỊNH LÍ
Nếu điểm A nằm ngoài mặt cầu S(O ; R) thì qua A có vô số tiếp tuyến với mặt cầu. Khi đó
a) Độ dài các đoạn thẳng nối A với các tiếp điểm đều bằng nhau.
b) Tập hợp các tiếp điểm là một đường tròn nằm trên mặt cầu.

Lấy một mặt phẳng bất kì đi qua AO, nó cắt mặt cầu S(O ; R) theo một đường tròn (C) (h.35). Gọi AH là một tiếp tuyến của đường tròn đó tại H. Chứng minh rằng AH cũng tiếp xúc với mặt cầu tại điểm H.
a) Tính độ dài đoạn AH theo R và d=OA.
b) Kẻ HI vuông góc với OA tại I rồi chứng minh rằng I là điểm cố định không phụ thuộc vào tiếp tuyến AH. Từ đó suy ra kết luận b) trong định lí.
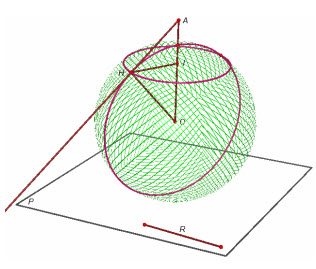
Hình 35
4. Diện tích mặt cầu và thể tích khối cầu
Ta đã biết thế nào là diện tích của các đa giác phẳng. Ta định nghĩa diện tích của hình đa diện là tổng diện tích các mặt của nó.
Tuy mặt cầu không giống như hình đa diện vì nó không phải là hợp của các đa giác, nhưng hiển nhiên là nó cũng phải có một “diện tích” nào đó. Nếu để sơn một mặt cầu, ta phải dùng 1kg sơn và cũng 1kg sơn loại đó, ta có thể sơn được hình chữ nhật (với độ mỏng của lớp sơn như nhau) thì có thể xem diện tích của mặt cầu bằng diện tích hình chữ nhật.
Sau đây ta nêu ra cách định nghĩa diện tích của mặt cầu và nói rõ hơn về công thức tính diện tích đó. Cũng tương tự như vậy đối với thể tích của khối cầu.
Khái niệm về diện tích mặt cầu và thể tích khối cầu
Cho mặt cầu đường kính AB (h.36).
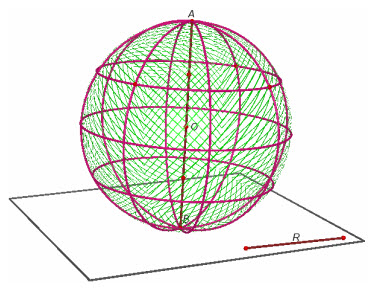
Hình 36
Mỗi nửa mặt phẳng có bờ là đường thẳng AB cắt mặt cầu theo một nửa đường tròn đường kính AB. Ta gọi các nửa đường tròn đó là các kinh tuyến ứng với đường kính AB.
Mỗi mặt phẳng vuông góc với AB nếu cắt mặt cầu theo một đường tròn thì đường tròn đó gọi là vĩ tuyến ứng với đường kính AB.
Nếu xem bề mặt Trái Đất là một mặt cầu có cực bắc là A, cực nam là B thì các kinh tuyến, vĩ tuyến nói trên chính là các kinh tuyến, vĩ tuyến của Trái Đất.
Chúng ta hãy lấy một số kinh tuyến và vĩ tuyến ứng với đường kính AB của mặt cầu. Chúng sẽ chia mặt cầu thành nhiều mảnh, có thể gọi mỗi mảnh đó là một “tứ giác cầu” (đặc biệt có thể là “tam giác cầu”). Ta có thể thấy rằng bốn đỉnh của một “tứ giác cầu” nằm trên một mặt phẳng và do đó cũng là bốn đỉnh của một tứ giác phẳng (đúng ra là hình thang cân) mà ta sẽ gọi là “xấp xỉ phẳng” của tứ giác cầu đang xét. Tương tư, mỗi “tam giác cầu” cũng có “xấp xỉ phẳng” là một tam giác cân. Tập hợp các “xấp xỉ phẳng” của tứ giác cầu và tam giác cầu làm thành một hình đa diện
Người ta chứng minh được rằng :
1) Khi độ dài các cạnh của
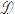
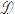
2) Khi độ dài các cạnh của
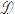
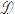
Các công thức
Dựa vào định nghĩa trên và dùng phương pháp giới hạn, người ta chứng minh được các công thức về diện tích của mặt cầu và thể tích của khối cầu như sau :
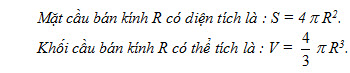
Câu hỏi và bài tập
1. Trong không gian cho ba đoạn thẳng AB, BC, CD sao cho AB⊥BC, BC⊥CD, CD⊥AB. Chứng minh rằng có mặt cầu đi qua bốn điểm A, B, C, D. Tính bán kính mặt cầu đó nếu AB = a, BC = b, CD = c.
2. a) Tìm tập hợp tâm các mặt cầu đi qua hai điểm phân biệt A, B cho trước.
b) Tìm tập hợp tâm các mặt cầu đi qua ba điểm phân biệt A, B, C cho trước.
c) Tìm tập hợp tâm các mặt cầu đi qua một đường tròn cho trước.
d) Có hay không một mặt cầu đi qua một đường tròn và một điểm nằm ngoài mặt phẳng chứa đường tròn ?
3. Cho điểm M nằm trong mặt cầu (S). Trong các mệnh đề sau đây, mệnh đề nào đúng ?
a) Mọi mặt phẳng đi qua M đều cắt (S) theo một đường tròn ;
b) Mọi đường thẳng đi qua M đều căt (S) tại hai điểm phân biệt.
4. Cho đường thẳng d và điểm A không nằm trên d. Xét các mặt cầu đi qua A và có tâm nằm trên d. Chứng minh rằng các mặt cầu đó luôn đi qua một đường tròn cố định.
5. Trong các mệnh đề sau đây, mệnh đề nào đúng ?
a) Nếu hình đa diện nội tiếp thì mọi mặt phẳng của nó là đa giác nội tiếp đường tròn ;
b) Nếu tất cả các mặt của một hình đa diện nội tiếp đường tròn thì đa diện đó nội tiếp mặt cầu.
6. a) Tìm tập hợp các tâm các mặt cầu tiếp xúc với ba cạnh của một tam giác cho trước.
b) Chứng minh rằng nếu có mặt cầu tiếp xúc với sáu cạnh của hình tứ diện ABCD thì
AB + CD = AC + BD = AD + BC.
7. a) Tính thể tích khối cầu ngoại tiếp hình chóp tam giác đều có cạnh đáy bằng a và chiều cao bằng h.
b) Cho hình chóp tứ giác đều S.ABCD có tất cả các cạnh đều bằng a. Gọi A[SUP]’[/SUP], B[SUP]’[/SUP], C[SUP]’[/SUP], D[SUP]’[/SUP] lần lượt là trung điểm các cạnh SA, SB, SC, SD. Chứng minh rằng các điểm A, B, C, D, A[SUP]’[/SUP], B[SUP]’[/SUP], C[SUP]’[/SUP], D[SUP]’[/SUP] cùng thuộc một mặt cầu và tính thể tích khối cầu đó.
8. Cho tứ diện ABCD với AB = CD = c, AC = BD =b, AD = BC = a.
a) Tính diện tích của mặt cầu ngoại tiếp tứ diện.
b) Chứng minh rằng có một mặt cầu tiếp xúc với bốn mặt của hình tứ diện (nó được gọi là mặt cầu nội tiếp tứ diện).
9. Tính diện mặt cầu ngoại tiếp hình chóp S.ABC biết rằng SA = a, SB = b, SC = c và ba cạnh SA, SB, SC đôi một vuông góc. Chứng minh rằng điểm S, trọng tâm tam giác ABC và tâm mặt cầu ngoại tiếp hình chóp S.ABC thẳng hàng.
10. a) Chứng minh rằng một hình lăng trụ có mặt cầu ngoại tiếp khi và chỉ khi nó là hình lăng trụ đứng với đáy là đa giác nội tiếp đường tròn.
b) Trong số các hình hộp nội tiếp mặt cầu cho trước, hình hộp nào có diện tích toàn phần lớn nhất ?
NGUỒN: SƯU TẦM
