Toán 10- Nâng Cao - Chương 3 - BÀI 1. PHƯƠNG TRÌNH TỔNG QUÁT CỦA ĐƯỜNG THẲNG
CHƯƠNG III. PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG
Bằng cách đưa vào mặt phẳng một hệ trục tọa độ, mỗi vectơ, mỗi điểm trên mặt phẳng đó đều được xác định bởi tọa độ của nó. Khi đó chúng ta có thể chuyển nhiều bài toán hình học sang bài toán đại số và ngược lại, từ kết quả của đại số suy ra được một số tính chất và mối quan hệ giữa các hình hình học.

- Lập được phương trình đường thẳng, đường tròn, đường cônic khi biết các yếu tố xác định mỗi đường.
- Nhớ và vận dụng được các biểu thức tọa độ vào việc tính khoảng cách, tính góc.
BÀI 1. PHƯƠNG TRÌNH TỔNG QUÁT CỦA ĐƯỜNG THẲNG
1. Phương trình tổng quát của đường thẳng
Trên hình 65, ta có các vectơ
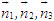
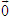

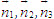
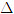

ĐỊNH NGHĨA
Vectơ
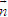

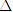

?1 Mỗi đường thẳng có bao nhiêu vectơ pháp tuyến? Chúng liên hệ với nhau như thế nào?
?2 Cho điểm I và vectơ
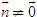
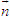
Bài toán
Trong mặt phẳng tọa độ, cho điểm I(x[SUB]0[/SUB], y[SUB]0[/SUB]) và vectơ . Gọi
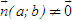
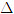
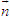
Giải. (h. 66)
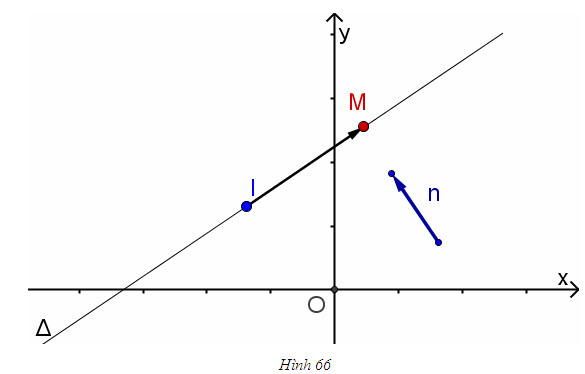
Điểm Mnằm trên

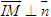
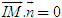
Ta có
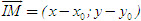
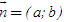
a(x – x[SUB]0[/SUB]) + b(y – y[SUB]0[/SUB]) = 0(1)
Đây chính là điều kiện cần và đủ để M(x ; y) nằm trên

Biến đổi (1) về dạng ax + by – ax[SUB]0[/SUB] – by[SUB]0[/SUB] = 0 và đặt –ax[SUB]0[/SUB] – by[SUB]0[/SUB] = c, ta được phương trình
ax + by + c = 0 (a[SUP]2[/SUP] + b[SUP]2[/SUP]≠ 0)
và gọi là phương trình tổng quátcủa đường thẳng

Tóm lại,

Ngược lại, ta có thể chứng minh được rằng: Mỗi phương trình dạng
ax + by + c = 0, với(a[SUP]2[/SUP] + b[SUP]2[/SUP] ≠ 0)
đều là phương trình tổng quát của một đường thẳng xác định, nhận
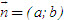
?3Mỗi phương trình sau có phải là phương trình tổng quát của đường thẳng không? Hãy chỉ ra một vectơ pháp tuyến của đường thẳng đó:
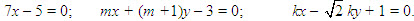

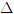
a) Hãy chỉ ra một vectơ pháp tuyến của đường thẳng

b) Trong các điểm sau đây, điểm nào thuộc


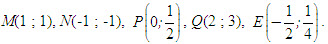
Ví dụ. Cho tam giác có ba đỉnh A = (-1 ; -1), B = (-1 ; 3), C = (2 ; -4). Viết phương trình tổng quát của đường cao kẻ từ A.
Giải. Đường cao cần tìm là đường thẳng đi qua A và nhận
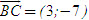
Các dạng đặc biệt của phương trình tổng quát

GHI NHỚ
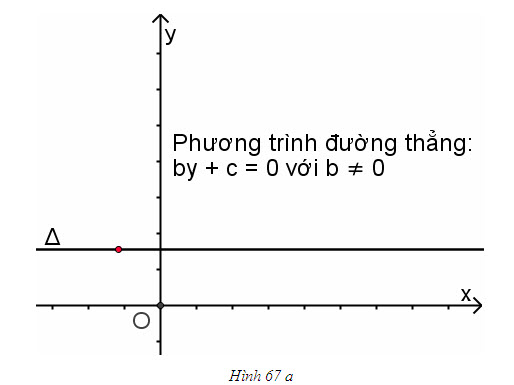
Đường thẳng by + c = 0 song song hoặc trùng với trục Ox (h. 67a).
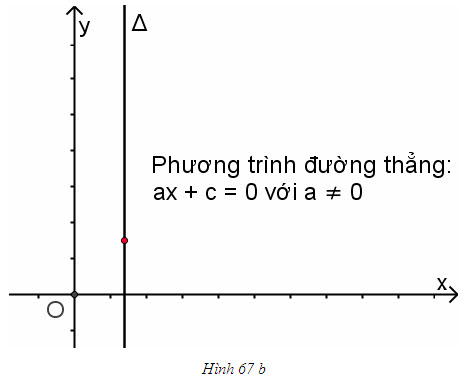
Đường thẳng ax + c = 0 song song hoặc trùng với trục Oy (h. 67b).
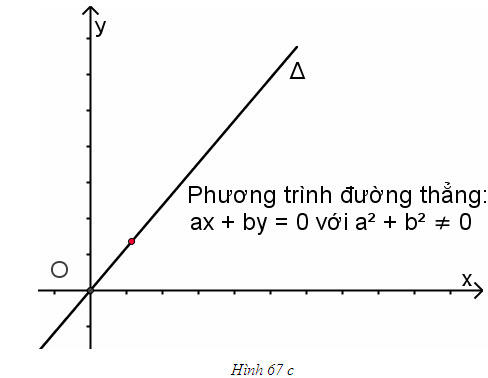
Đường thẳng ax + by = 0 đi qua gốc tọa độ (h. 67c).

a) Hãy viết phương trình tổng quát của đường thẳng

b) Chứng tỏ rằng phương trình tổng quát của
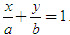
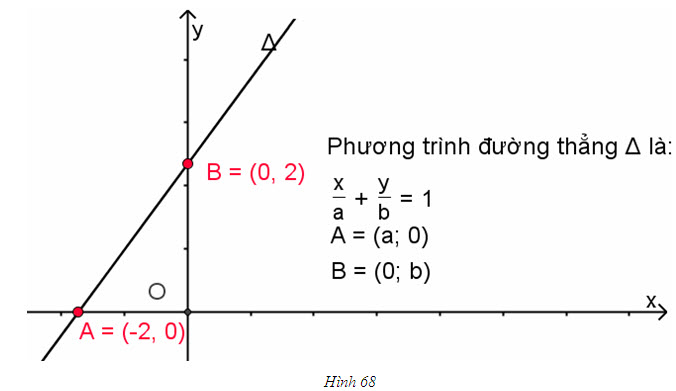
GHI NHỚ
Đường thẳng có phương trình
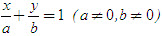
đi qua hai điểm A(a ; 0) và B(0 ; b).
Phương trình dạng (2) được gọi là phương trình đường thẳng theo đoạn chắn
?4Viết phương trình tổng quát của đường thẳng đi qua A(-1 ; 0) và B(0 ; 2).
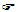
Xét đường thẳng

Nếu b ≠ 0 thì phương trình trên đưa được về dạng
y = kx + m(3)
với
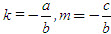


Ý nghĩa hình học của hệ số góc (h. 69)
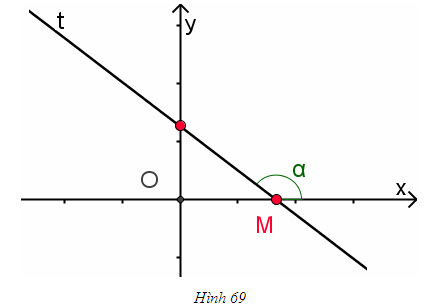
Xét đường thẳng

Với k ≠ 0, gọi M là giao điểm của

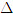
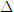
Khi k= 0 thì
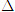
?5. Mỗi đường thẳng sau đây có hệ số góc bằng bao nhiêu? Hãy chỉ ra góc α tương ứng với hệ số góc đó.

2. Vị trí tương đối của hai đường thẳng
Trong mặt phẳng tọa độ, cho hai đường thẳng
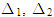
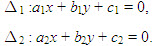
a) Hai đường thẳng
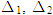
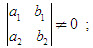
b) Hai đường thẳng
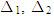

Hoặc
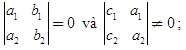
c) Hai đường thẳng
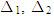
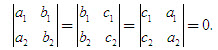
Trong trường hợp a[SUB]2[/SUB], b[SUB]2[/SUB], c[SUB]2[/SUB] đều khác 0, ta có

?6.Từ tỉ lệ thức
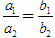
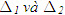
?7. Xét vị trí tương đối của hai đường thẳng
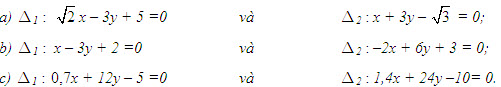
Câu hỏi và bài tập
1. Trong các mệnh đề sau, mệnh đề nào đúng?
a) Đường thẳng song song với trục Ox có phương trình y = m (m ≠ 0);
b) Đường thẳng có phương trình x = m[SUP]2[/SUP] + 1 song song với trục Oy;
c) Phương trình y = kx + b là phương trình của đường thẳng;
d) Mọi đường tròn đều có phương trình dạng y = kx + b.
e) Đường thẳng đi qua hai điểm A(a; 0) và B(0 ; b) có phương trình
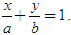
2.Viết phương trình tổng quát của
a) Đường thẳng Ox ;
b) Đường thẳng Oy ;
c) Đường thẳng đi qua M(x[SUB]0[/SUB] ; y[SUB]0[/SUB]) và song song với Ox ;
d) Đường thẳng đi qua M(x[SUB]0[/SUB] ; y[SUB]0[/SUB]) và vuông gócvới Ox ;
e) Đường thẳng OM, với M(x[SUB]0[/SUB] ; y[SUB]0[/SUB]) khác điểm O.
3. Cho tam giác ABC có phương trình các đường thẳng AB, BC, CA là
AB : 2x – 3y – 1 = 0;
BC : x + 3y + 7 = 0;
CA :5x – 2y + 1 = 0.
Viết phương trình tổng quát của đường cao kẻ từ đỉnh B.
4.Cho hai điểm P(4 ; 0), Q(0 ; -2).
a) Viết phương trình tổng quát của đường thẳng đi qua điểm A(3 ; 2) và song song với đường thẳng PQ;
b) Viết phương trình tổng quát của đường trung trực của đoạn thẳng PQ.
5.Cho đường thẳng d có phương trình x – y = 0 và điểm M(2 ; 1).
a) Viết phương trình tổng quát của đường thẳng đối xứng với đường thẳng d qua điểm M.
b) Tìm hình chiếu của điểm M trên đường thẳng d.
6. Xét vị trí tương đối của mỗi cặp đường thẳng sau và tìm giao điểm (nếu có) của chúng
a) 2x– 5y + 3 = 0 và 5x + 2y – 3 = 0 ;
b) x– 3y + 4 = 0 và 0,5x – 1,5y + 4 = 0 ;
c) 10x+ 2y – 3 = 0 và 5x + y – 1,5 = 0 ;
SƯU TẦM
