Hình 10: Bài 6: Đường Hypebol

[Thandieu2]

Toán 10- Nâng Cao - Chương 3 - BÀI 6. ĐƯỜNG HYPEBOL
​

BÀI 6. ĐƯỜNG HYPEBOL

​

Đường hypebol cũng là một đường quen thuộc đối với chúng ta, chẳng hạn
- Đồ thị của hàm số

là một đường hypebol (h. 86a);
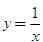
- Quan sát vùng sáng hắt lên bức tường từ một đèn bàn ; vùng sáng này có hai mảng, mỗi mảng được giới hạn bởi một phần của một đường hypebol (h. 86b).

​

1. Định nghĩa đường hypebol

ĐỊNH NGHĨA
Cho hai điểm cố định F[SUB]1[/SUB], F[SUB]2[/SUB] có khoảng cách F[SUB]1[/SUB]F[SUB]2[/SUB] = 2c (c > 0). Đường hypebol (còn gọi là hypebol) là tập hợp các điểm M sao cho

, trong đó a là số dương cho trước nhỏ hơn c (h. 87).
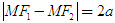
Hai điểm F[SUB]1[/SUB] và F[SUB]2[/SUB] gọi là các tiêu điêmcủa hypebo. Khoảng cách F[SUB]1[/SUB]F[SUB]2[/SUB] = 2c gọi là tiêu cự của hypebol.

​

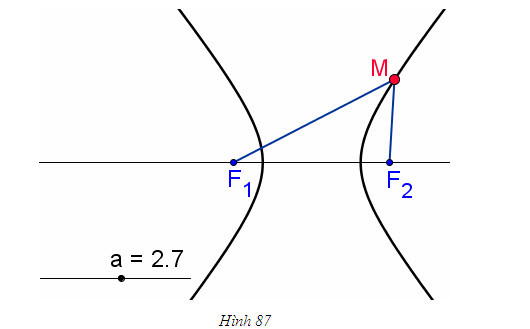
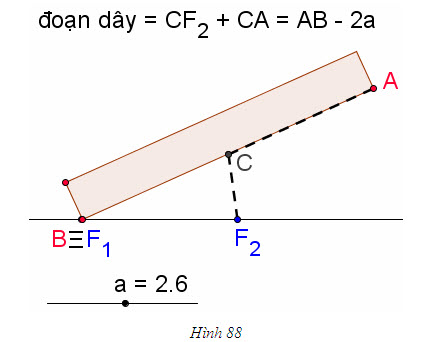
Có thể vẽ hypebol như sau (h. 88) : Lấy một thước thẳng có mép AB và một sợi dây không đàn hồi có chiều dài l nhỏ hơn chiều dài AB của thước và l > AB – F[SUB]1[/SUB]F[SUB]2[/SUB]. Đóng hai chiếc đinh lên mặt một bảng gỗ tại F[SUB]1[/SUB], F[SUB]2[/SUB]. Đính một đầu dây vào điểm A và đầu dây kia vào F[SUB]2[/SUB]. Đặt thước sao cho sợi dây luôn bị căng rồi cho thước quay quanh F[SUB]1[/SUB], mép thước luôn áp sát mặt gỗ. Khi đó, đầu bút chì C sẽ vạch nên một đường cong. Ta sẽ chứng tỏ đường cong đó là một phần của đường hypebol. Thật vậy, ta có
CF[SUB]1[/SUB] – CF[SUB]2[/SUB] = (CF[SUB]1[/SUB]+ CA) – (CF[SUB]2[/SUB] + CA) – AB – l không đổi.

​

2. Phương trình chính tắc của hypebol

Cho hypebol (H) như trong định nghĩa trên. Ta chọn hệ trục tọa độ Oxy có gốc là trung điểm của đoạn thẳng F[SUB]1[/SUB]F[SUB]2[/SUB], trục Oy là đường trung trực của F[SUB]1[/SUB]F[SUB]2[/SUB] và F[SUB]2[/SUB] nằm trên tia Ox.
Khi đó F[SUB]1[/SUB]= (–c ; 0), F[SUB]2[/SUB] = (c ; 0) (h. 89).

​

1.Giả sử điểm M(x ; y) nằm trên hypebol (H). Hãy tính biểu thức

và sử dụng giả thiết

để suy ra

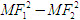
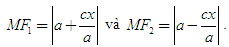
Các đoạn thẳng MF[SUB]1[/SUB], MF[SUB]2[/SUB]được gọi là bán kính qua tiêu của điểm M.

Bây giờ ta sẽ lập phương trình của hypebol (H) đối với hệ tọa độ đã chọn.
Ta có

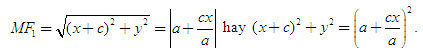
Rút gọn đẳng thức trên ta được

Chú ý rằng a[SUP]2[/SUP]– c[SUP]2[/SUP] < 0 nên ta có thể đặt a[SUP]2[/SUP] – c[SUP]2[/SUP] = b[SUP]2[/SUP]hay b[SUP]2[/SUP]= a[SUP]2[/SUP] – c[SUP]2[/SUP] với (b > 0), và ta được

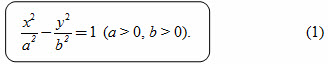
Ngược lại, có thể chứng minh được rằng : nếu điểm M có tọa độ (x ;y) thỏa mãn (1) thì

và do đó

, tức là Mthuộc hypebol (H).
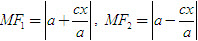
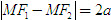
Phương trình (1) được gọi là phương trình chính tắc của hypebol.

3. Hình dạng của hypebol

2.Từ phương trình chính tắc (1) của hypebol, hãy giải thích vì sao nócó các tính chất sau
a) Gốc tọa độ O là tâm đối xứng của hypebol. Ox, Oy là hai trục đối xứng của hypebol.
b) Hypebol cắt trục Ox tại hai điểm và không cắt trục Oy.
Ngoài ra, đối với hypebol có phương trình chính tắc (1), ta còn có các khái niệm sau đây.
Trục Ox(chứa hai tiêu điểm) gọi là trục thực, trục Oy gọi là trục ảo của hypebol. Hai giao điểm của hypebol với trục Ox gọi là hai đỉnhcủa hypebol. Người ta cũng gọi đoạn thẳng nối hai đỉnh của hypebol là trục thực. Khoảng cách 2a giữa hai đỉnh gọi là độ dài trục thực, 2b gọi là độ dài trục ảo.
- Hypebol gồm hai phần nằm hai bên trục ảo, mỗi phần gọi là một nhánh của hypebol.
- Ta cũng gọi, giống như với elip, tỉ số giữa tiêu cự và độ dài trục thực là tâm sai của hypebol, kí hiêu là e, tức là

. Chú ý rằng ta luôn có e> 1.

Ví dụ. Cho hypebol (H) :

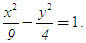
Xác định tọa độ các đỉnh, các tiêu điểm và tính tâm sai, độ dài trục thực, độ dài trục ảo của (H).
Giải. Hypebol (H) có a[SUP]2[/SUP] = 9, b[SUP]2[/SUP] = 4 nên a = 3, b = 2, c[SUP]2[/SUP] = a[SUP]2[/SUP] + b[SUP]2[/SUP] = 13,

. Vậy Hypebol (H) có các tiêu điểm (–

các đỉnh A[SUB]1[/SUB](–3 ; 0), A[SUB]2[/SUB](3 ; 0) ; tâm sai

; độ dài trục thực 2a= 6; độ dài trục ảo 2b = 4.
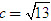
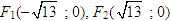
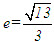
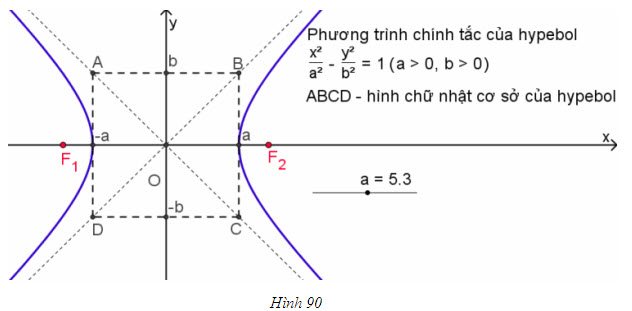
- Hình chữ nhật tạo bởi các đường thẳng x = ± a, y = ± b gọi là hình chữ nhật cơ sở của hypebol có phương trình (1) (h. 90). Hai đường thẳng chứa hai đường chéo của hình chữ nhật cơ sở gọi là hai đường tiệm cận của hypebol. Phương trình hai đường tiệm cận đó là

​

3.Cho hypebol (H) :

. Lấy điểm M(x[SUB]0[/SUB]; y[SUB]0[/SUB]) trên (H) với x[SUB]0[/SUB] > 0, y[SUB]0[/SUB]> 0. Chứng tỏ rằng khoảng cách từ Mđến đường tiệm cận

bằng

.
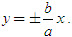
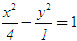
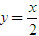
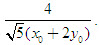
Nhận xét gì về khoảng cách đó khhi x[SUB]0[/SUB] tăng dần?
Như vậy, khi điểm M trên hypebol càng xa gốc tọa độ thì khoảng cách từ điểm đó đến một trong hai đường tiệm cận càng nhỏ đi, điều đó cũng có nghĩa là điểm M ngày càng gần sát đường tiệm cận đó (điều này giải thích ý nghĩa của từ “tiệm cận”).


Em có biết?

Hai đường tròn không đồng tâm (O ;R) và(O’ ; R’) có điểm chung M thì hiển nhiên |MO – MO’|=|r – R’|, nên khi giữ O, O’ cố định và cho R, R’ thay đổi sao cho |R – R’| = 2a không đổi (a > 0) thì các giao điểm M cùng nằm trên một hypebol với tiêu điểm là O và O’.
Hình 91 minh họa những hypebol như thế với các giá trị khác nhau của a.

​

Câu hỏi và bài tập
36. Cho hypebol (H) có phương trình chính tắc

. Hỏi trong các mệnh đề sau, mệnh đề nào đúng?
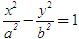
a) Tiêu cự của (H) là 2c, trong đó c[SUP]2[/SUP] = a[SUP]2[/SUP] + b[SUP]2[/SUP].
b) (H) có độ dài trục thực bằng 2a, độ dài trục ảo bằng 2b.
c) Phương trình hai đường tiệm cận của (H) là

.
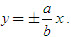
d) Tâm sai của (H) là

.

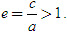
37. Tìm tọa độ các tiêu điểm, các đỉnh ; độ dài trục thực, trục ảo và phương trình các đường tiệm cận của mỗi hypebol có phương trình sau

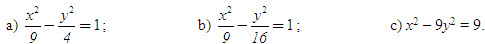
38. Cho đường tròn (C) tâm F[SUB]1[/SUB], bán kính R và một điểm F[SUB]2[/SUB] ở ngoài (C). Chứng minh rằng tập hợp các đường tròn đi qua F[SUB]2[/SUB], tiếp xúc với (C) là một đường hypebol. Viết phương trình chính tắc của hypebol đó.

39. Viết phương trình chính tắc của hypebol (H) trong mỗi trường hợp sau
a) (H) có một tiêu điểm là (5 ; 0) và độ dài trục thực bằng 8;
b) (H) có tiêu cự bằng

, một đường tiệm cận là

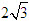
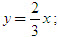
c) (H) có tâm sai e =

và đi qua điểm (

; 6).

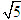
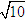
40. Chứng minh rằng tích các khoảng cách từ một điểm bất kì thuộc hypebol đến hai đường tiệm cận của nó là một số không đổi.

41. Trong mặt phẳng tọa độ cho hai điểm

. Chứng minh rằng với mỗi điểm M(x ; y) nằm trên đồ thị hàm số

, ta đều có

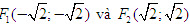
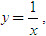
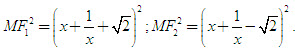
Từ đó suy ra

.


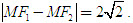
SƯU TẦM