Toán 12 - Chương III - Bài 1. Hệ tọa độ trong không gian
Ở lớp 10, chúng ta đã làm quen với phương pháp tọa độ trên mặt phẳng. Trong chương này, ta sẽ nói đến phương pháp tọa độ trong không gian.
Học xong chương này, học sinh cần:
- Hiểu và nắm vững định nghĩa về tọa độ của điểm và của vectơ trong một hệ trục tọa độ.
- Nhớ và vận dụng được biểu thức tọa độ của các phép tính trên các vectơ, các công thức và cách tính các đại lượng hình học bằng tọa độ.
- Nhận dạng các phương trình đường thẳng, mặt phẳng, mặt cầu trong một hệ tọa độ cho trước và viết được phương trình của chúng khi biết một số điều kiện cho trước.
1. Hệ trục tọa độ trong không gian
Trong hình học phẳng, ta đã biết hệ trục tọa độ trên mặt phẳng. Hệ đó được kí hiệu là Oxy hoặc
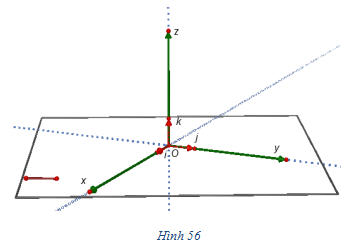
Trong không gian, xét ba trục tọa độ Ox, Oy, Oz có chung điểm gốc O và đôi một vuông góc với nhau (h.56).
ĐỊNH NGHĨA 1
Hệ gồm ba trục Ox, Oy, Oz đôi một vuông góc được gọi là hệ trục tọa độ vuông góc trong không gian.
Thuật ngữ và kí hiệu
Hệ trục tọa độ trong định nghĩa trên còn được gọi đơn giản là hệ tọa độ trong không gian, và kí hiệu Oxyz. Ta thường gọi các vectơ đơn vị trên các trục Ox, Oy, Oz lần lượt là
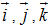
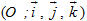
Điểm O gọi là gốc của hệ tọa độ, hoặc đơn giản là gốc tọa độ, Ox gọi là trục hoành, Oy gọi là trục tung, Oz gọi là trục cao.
Các mặt phẳng đi qua hai trong ba trục tọa độ gọi là các mặt phẳng tọa độ, ta kí hiệu chúng là mp(Oxy), mp(Oyz), mp(Oxz), hoặc đơn giản là (Oxy), (Oyz), (Oxz).
Khi không gian đã có một hệ tọa độ Oxyz thì nó được gọi là không gian tọa độ Oxyz hoặc đơn giản là không gian Oxyz.
Ta cần chú ý tới các đẳng thức sau đây :
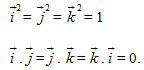
?1Tại sao ta có các đẳng thức trên ?
2. Tọa độ của vectơ
Trong không gian tọa độ Oxyz với các vectơ đơn vị
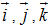
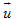
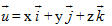
Bộ ba số đó cũng được gọi là tọa độ của vectơ
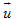
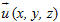
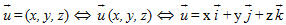
Hiển nhiên theo định nghĩa và kí hiệu trên, ta có
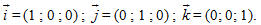
?2 Tại sao nếu vectơ
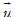
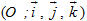
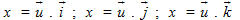
3. Tọa độ của điểm
Trong không gian tọa độ Oxyz, mỗi điểm M được hoàn toàn xác định bởi vectơ
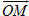
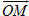
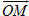
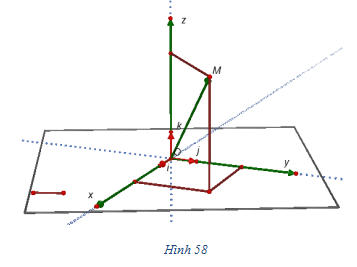
Như vậy:
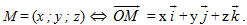
Nếu điểm M có tọa độ (x ; y ; z) thì số x gọi làhoành độ, số y gọi là tung độ và số z gọi là cao độ của điểm M.
?3 Cho hệ tọa độ Oxyz và điểm M (x ; y ; z). Tại sao có các khẳng định như sau ?
a) M
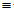
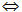
b) M
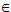
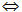
M
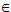
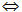
M
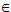
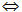
?4 Với điều kiện nào của x, y, z thì điểm M (x, y, z) nằm trên một trục tọa độ ?
1
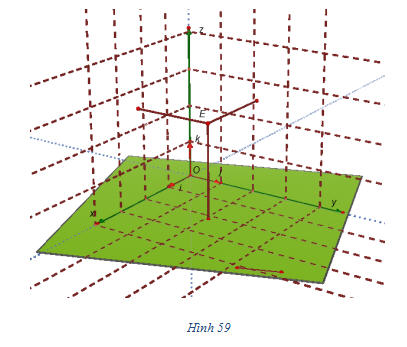
Trên hình 59 có một hệ trục tọa độ Oxyz cùng với các hình vuông có cạnh bằng đơn vị.
a) Xác định tọa độ các điểm A, B, C, D, E.
b) Dựng điểm P nếu P= (3 ; 6; -3).
4. Liên hệ giữa tọa độ của vectơ và tọa độ của hai điểm mút
Cho hai điểm A(x[SUB]A[/SUB] ; y[SUB]A[/SUB] ; z[SUB]A[/SUB]) và B(x[SUB]B[/SUB] ; y[SUB]B[/SUB] ; z[SUB]B[/SUB]). Theo định nghĩa ta có
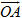
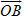
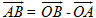
Từ đó ta suy ra tọa độ của vectơ
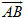
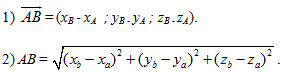
2
Trong không gian tọa độ Oxyz cho bốn điểm không đồng phẳng A(x[SUB]A[/SUB] ; y[SUB]A[/SUB] ; z[SUB]A[/SUB]), B(x[SUB]B[/SUB] ; y[SUB]B[/SUB] ; z[SUB]B[/SUB]), C(x[SUB]C[/SUB] ; y[SUB]C[/SUB] ; z[SUB]C[/SUB]), D(x[SUB]D[/SUB] ; y[SUB]D[/SUB] ; z[SUB]D[/SUB]).
a) Tìm tọa độ trung điểm của đoạn thẳng AB.
b) Tìm tọa độ trọng tâm của tam giác ABC.
c) Tìm tọa độ trọng tâm của tứ diện ABCD.
5. Tích có hướng của hai vectơ
Ta đã biết về tích vô hướng của hai vectơ. Ta cần nhớ rằng tích đó là một số và có thể tính được dễ dàng nếu biết tọa độ của hai vectơ.
Sau đây ta sẽ nói về tích có hướng của hai vectơ.
Khác với tich vô hướng, tích có hướng không phải là một số mà là một vevtơ, bởi vậy tích có hướng còn được gọi là tích vectơ.
ĐỊNH NGHĨA 2
Tích có hướng (hay tích vectơ) của hai vectơ
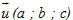
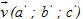
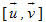
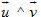
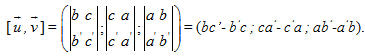
Ví dụ 3. Cho

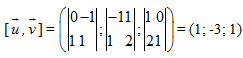
3
Đối với hệ tọa độ
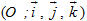
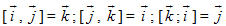
Tính chất của tích có hướng
Các tính chất sau đây của tích có hướng thường được áp dụng khi giải một bài toán hình học :

Chứng minh
1. Giả sử
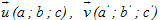
Từ định nghĩa từ tích có hướng ta có
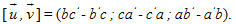
Suy ra
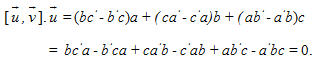
2. Nếu một trong hai vectơ
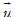

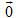
Bây giờ ta xét trường hợp cả hai vectơ đó khác
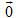
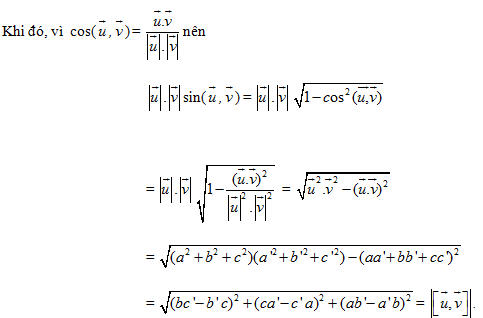
3. Tính chất này được suy ra trực tiếp từ tính chất 2.
CHÚ Ý
Ta vẽ các vectơ
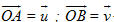
Nếu hai vectơ
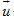
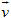
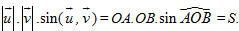
Vậy độ dài của vectơ
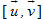

Ứng dụng của tích có hướng
a) Tính diện tích hình bình hành
Nếu ABCD là hình bình hành thì theo chú ý trên, ta có
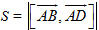
b) Tính thể tích khối hộp
Nếu ABCD.A’B’C’D’ là hình hộp với diện tích đáy ABCD là S, chiều cao là h = AH,
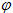
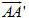
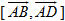
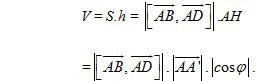
Vậy
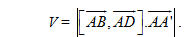
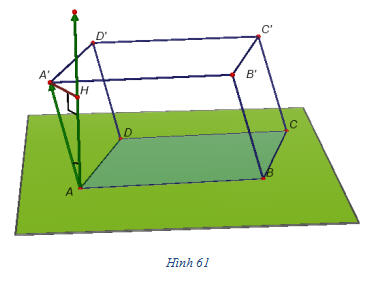
4
Hãy chứng tỏ rằng ba vectơ
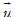

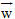
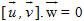
Như vậy, chúng ta nên nhớ một số tính chất liên quan đến tích vô hướng và tích có hướng sau đây
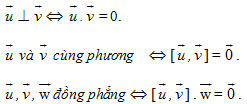
6. Phương trình mặt cầu
Trong không gian tọa độ Oxyz cho mặt cầu S(I ; R) có tâm I(x[SUB]0[/SUB] ; y[SUB]0[/SUB] ; z[SUB]0[/SUB]) và bán kính R (h.62).

Điểm M(x, y, z) thuộc mặt cầu đó khi và chỉ khi IM = R hay IM[SUP]2[/SUP] = R[SUP]2[/SUP], nghĩa là (x - x[SUB]0[/SUB])[SUP]2[/SUP]+(y - y[SUB]0[/SUB])[SUP]2[/SUP]+(z - z[SUB]0[/SUB])[SUP]2[/SUP] = R[SUP]2[/SUP].
Phương trình trên được gọi là phương trình của mặt cầu S(I ; R).
Như vậy, nếu biết tọa độ của tâm và biết bán kính mặt cầu thì ta có thể dễ dàng viết được phương trình của mặt cầu đó.
Mặt cầu tâm I(x[SUB]0[/SUB] ; y[SUB]0[/SUB] ; z[SUB]0[/SUB]), bán kính R có phương trình
(x - x[SUB]0[/SUB])[SUP]2[/SUP]+(y - y[SUB]0[/SUB])[SUP]2[/SUP]+(z - z[SUB]0[/SUB])[SUP]2[/SUP] = R[SUP]2[/SUP].
5
Hãy viết phương trình mặt cầu có đường kính A[SUB]1[/SUB]A[SUB]2[/SUB] với
A[SUB]1[/SUB] = (a[SUB]1[/SUB] ; b[SUB]1[/SUB] ; c[SUB]1[/SUB]) và A[SUB]2[/SUB] = (a[SUB]2[/SUB] ; b[SUB]2[/SUB] ; c[SUB]2[/SUB])
Theo hai cách :
- Tìm tọa độ tâm và tính bán kính của mặt cầu.
- Nhận xét rằng điểm M nằm trên mặt cầu khi và chỉ khi
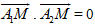
6
Viết phương trình đi qua bốn điểm A(0; 0; 0), B(1; 0; 0), C(0; 1; 0), D(0; 0; 1).
Nhận xét. Nếu ta triển khai phương trình mặt cầu S(I. R) và viết dưới dạng f(x, y, z) = 0 thì dễ thấy rằng f(x, y, z) là đa thức bậc hai đối với x, y, z có các hệ số của x[SUP]2[/SUP], y[SUP]2[/SUP], z[SUP]2[/SUP] đều bằng 1 và không có các dạng tử chứa xy, yz, zx.
Bây giờ ta xét vấn đề ngược lại : Phương trình dạng
x[SUP]2[/SUP] + y[SUP]2[/SUP] + z[SUP]2[/SUP] + 2ax + 2by + 2cz + d = 0 (1)
có phải là phương trình mặt cầu trong không gian tọa độ Oxyz cho trước hay không ?
Phương trình (1) có thể viết như sau :
(x + a)[SUP]2[/SUP] + (y + b)[SUP]2[/SUP] + (z + c)[SUP]2[/SUP] = a[SUP]2[/SUP] + b[SUP]2[/SUP] + c[SUP]2[/SUP] - d. (2)
Gọi I là điểm có tọa độ (-a ; -b ; -c) và M là điểm có tọa độ (x ; y ; z) thì vế trái của (2) chính là IM[SUP]2[/SUP]. Bởi vậy ta dễ dàng suy ra:
Nếu a[SUP]2[/SUP] + b[SUP]2[/SUP] + c[SUP]2[/SUP] - d > 0 thì
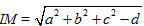
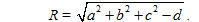
Nếu a[SUP]2[/SUP] + b[SUP]2[/SUP] + c[SUP]2[/SUP] - d = 0 thì IM = 0 và phương trình (1) xác định điểm I duy nhất.
Nếu a[SUP]2[/SUP] + b[SUP]2[/SUP] + c[SUP]2[/SUP] - d < 0 thì không có điểm M nào có tọa độ thỏa mãn (1).
Phương trình x[SUP]2[/SUP] + y[SUP]2[/SUP] +z[SUP]2[/SUP] + 2ax + 2by + 2cz + d = 0 là phương trình của mặt cầu khi và chỉ khi a[SUP]2[/SUP] + b[SUP]2[/SUP] + c[SUP]2[/SUP] > d. Khi đó tâm mặt cầu là điểm I(-a, -b, -c) và bán kính mặt cầu là
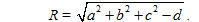
7
Mỗi phương trình sau đây có phải là phương trình mặt cầu hay không ? Nếu phải thì hãy xác định tâm và bán kính mặt cầu đó.
a) x[SUP]2[/SUP] + y[SUP]2[/SUP] - z[SUP]2[/SUP] + 2x - y + 1 = 0 ;
b) 3x[SUP]2[/SUP] + 3y[SUP]2[/SUP] + 3z[SUP]2[/SUP] – 2x = 0 ;
c) 2x[SUP]2[/SUP] + 2y[SUP]2[/SUP] = (x + y)[SUP]2[/SUP] – z[SUP]2[/SUP] + 2x – 1 ;
d) (x + y)[SUP]2[/SUP] = 2xy - z[SUP]2[/SUP] + 1.
Câu hỏi và bài tập
1. Cho các vectơ :
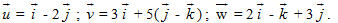
a) Tìm tọa độ của các vectơ đó.
b) Tìm côsin các góc:
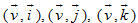
c) Tính các tích vô hướng
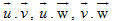
2. Cho vectơ
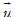
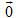
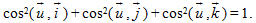
3. Tìm góc giữa hai vectơ
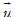

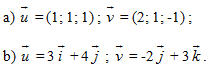
4. Biết
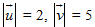
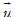

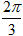
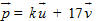
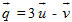
5.Cho điểm M(a, b, c).
a) Tìm tọa độ hình chiếu (vuông góc) của M trên các mặt phẳng tọa độ và trên các trục tọa độ.
b) Tìm các khoảng cách từ điểm M đến các mặt phẳng tọa độ, đến các trục tọa độ.
c) Tìm tọa độ các điểm đối xứng với M qua các mặt phẳng tọa độ.
6. Cho hai điểm A(x[SUB]1[/SUB], y[SUB]1[/SUB]¬, z[SUB]1[/SUB]) và B(x[SUB]2[/SUB], y[SUB]2[/SUB]¬, z[SUB]2[/SUB]). Tìm tọa độ điểm M chia đoạn thẳng AB theo tỉ số k (tức là
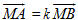
7. Cho hình bình hành ABCD với A(-3; -2; 0), B(3; -3; 1), C(5; 0; 2).
Tìm tọa độ đỉnh D và tính góc giữa hai vectơ
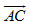
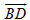
8. a) Tìm tọa độ điểm M thuộc trục Ox sao cho M cách đều hai điểm A(1; 2; 3) và B(-3; -3; 2).
b) Cho ba điểm A(2; 0; 4), B(4;
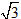
9. Xét sự đồng phẳng của ba vectơ
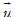

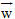
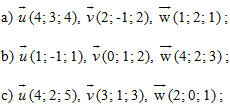
10. Cho ba điểm A(1; 0; 0), B(0; 0; 1), C(2; 1; 1).
a) Chứng minh A, B, C không thẳng hàng.
b) Tính chu vi và diện tích tam giác ABC.
c) Tính độ dài và đường cao của tam giác ABC kẻ từ đỉnh A.
d) Tính các góc của tam giác ABC.
11. Cho bốn điểm A(1; 0; 0), B(0; 1; 0), C(0; 0; 1) và D(-2; 1; -2).
a) Chứng minh rằng A, B, C, D là bốn đỉnh của một hình tứ diện.
b) Tính góc giữa các đường thẳng chứa các cạnh đối của tứ diện đó.
c) Tính thể tích tứ diện ABCD và độ dài đường cao của tứ diện kẻ từ đỉnh A.
12. Cho hình chóp S.ABC có đường cao SA = h, đáy là tam giác ABC vuông tại C, AC = b, BC = a. Gọi M là trung điểm của AC và N là điểm sao cho
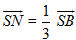
a) Tính độ dài đoạn thẳng MN.
b) Tìm sự liên hệ giữa a, b, h để MN vuông góc với SB.
13. Tìm tọa độ tâm và tính bán kính của mỗi mặt cầu sau đây :
a) x[SUP]2[/SUP] + y[SUP]2[/SUP] + z[SUP]2[/SUP] – 8x + 2y + 1 = 0 ;
b) 3x[SUP]2[/SUP] + 3y[SUP]2[/SUP] + 3z[SUP]2[/SUP] + 6 x - 2y + 15z - 2 = 0 ;
c) 9x[SUP]2[/SUP] + 9y[SUP]2[/SUP] + 9z[SUP]2[/SUP] – 6 x + 18y + 1 = 0 ;
14. Trong mỗi trường hợp sau, hãy viết phương trình mặt cầu :
a) Đi qua ba điểm A(0; 8; 0), B(4; 6; 2), C(0; 12; 4) và có tâm nằm trên mp(Oyz) ;
b) Có bán kính bằng 2, tiếp xúc với mặt phẳng (Oyz) và có tâm nằm trên tia Ox ;
c) Có tâm I(1; 2; 3) và tiếp xúc với mp(Oyz).
NGUỒN: SƯU TẦM
