Toán 12- Nâng Cao - Chương I - Bài 4 THỂ TÍCH CỦA KHỐI ĐA DIỆN
§4 THỂ TÍCH CỦA KHỐI ĐA DIỆN
1. Thế nào là thể tích của một khối đa diện ?
Chúng ta biết rằng trong mặt phẳng, mỗi đa giác có một diện tích. Đó là số đo phần mặt phẳng mà đa giác đó chiếm chỗ. Tương tự như vậy, các khối đa diện chiếm những phần không gian lớn nhỏ khác nhau. Thể tích của mỗi khối đa diện là số đo của phần không gian mà nó chiếm chỗ.
Chúng ta đã biết các công thức tính thể tích của một khối đa diện đơn giản. Sau đây chúng ta sẽ nói rõ hơn về các công thức này.
Để có những công thức như thế, chúng ta thừa nhận rằng mỗi khối đa điện có thể tích là một sốdương, thỏa mãn các tính chất sau đây :
1) Hai khối đa diện bằng nhau thì có thể tích bằng nhau.
2) Nếu một khối đa diện được phân chia thành nhiều khối đa diện nhỏ thì thể tích của nó bằng tổng thể tích của các khối đa diện nhỏ đó.
3) Khối lập phương có cạnh bằng 1 thì có thể tích bằng 1.
CHÚ Ý
1) Trong thực tế, khi phải đo lường và tính toán về độ dài, diện tích và thể tích, người ta thường dùng những đơn vị đo độ dài là 1cm chẳng hạn thì theo tính chất 3, khối lập phương có cạnh bằng 1 (hiểu là 1cm) sẽ có thể tích bằng 1, nhưng hiểu là 1cm[SUP]3[/SUP]. Tương tự, khối lập phương có cạnh 1dm sẽ có thể tích là 1dm[SUP]3[/SUP], khối lập phương có cạnh 1km thì có thể tích là 1km[SUP]3[/SUP],…
2) Đôi khi để đơn giản, thể tích của khối đa diện giới hạn bởi hình đa diện
2. Thể tích của khối hộp chữ nhật
Giả sử ta có một khối hộp chữ nhật với ba kích thước a, b, c đều là những số nguyên dương. Khi đó, bằng những mặt phẳng song song với các mặt của khối hộp, ta có thể phân chia nó thành các khối lập phương có cạnh bằng 1 (h.25).
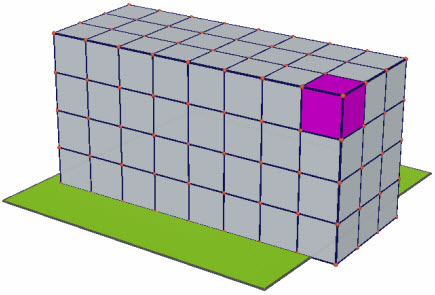
Hình 25
Hiển nhiên số các khối lập phương đó bằng tích số a.b.c.
Theo tính chất 2, thể tích V của khối hộp chữ nhật bằng tổng các thể tích của các khối lập phương và theo tính chất 3, mỗi khối lập phương đó có thể tích bằng 1. Từ đó ta suy ra công thức
V = abc.
Trong trường hợp các kích thước a, b, c của khối hộp chữ nhật là những số dương tùy ý (không nhất thiết phải là số nguyên), người ta chứng minh được rằng công thức nói trên vẫn đúng. Như vậy một cách tổng quát ,ta có :
ĐỊNH LÍ 1
Thể tích của một khối hộp chữ nhật bằng tích số của ba kích thước.
Ví dụ 1. Tính thể tích của khối lập phương có các đỉnh là trọng tâm các mặt của một khối tám mặt đều cạnh a.
Giải. Giả sử có khối tám mặt đều với các đỉnh là S, S[SUP]’[/SUP], A, B, C, D (h.26). Gọi M và N lần lượt là trọng tâm của tam giác SAB và SBC thì đoạn thẳng MN là một cạnh của khối lập phương. Gọi M[SUP]’[/SUP], N[SUP]’[/SUP] lần lượt là trung điểm của AB và BC thì M và N lần lượt nằm trên SM[SUP]’ [/SUP]và SN[SUP]’[/SUP] nên
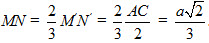
Vậy thể tích của khối lập phương là
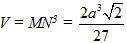
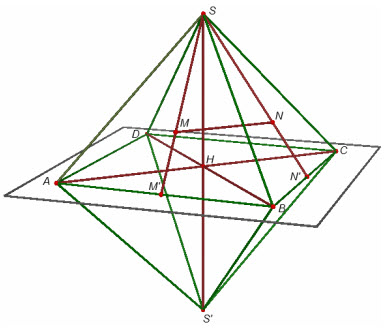
Hình 26
1: Cho khối lăng trụ đứng có chiều cao bằng h, đáy là tam giác vuông với hai cạnh góc vuông bằng a và b. Tính thể tích của khối lăng trụ đó.
3. Thể tích của khối chóp
Dùng phương pháp giới hạn, người ta có thể chứng minh được định lí sau đây.
ĐỊNH LÍ 2
Thể tích của một khối chóp bằng một phần ba tích số của diện tích mặt đáy và chiều cao của khối chóp đó.
Như vậy, nếu ta kí hiệu diện tích mặt đáy của khối chóp là S[SUB]đáy[/SUB] và chiều cao của khối chóp là h (h là khoảng cách từ đỉnh của khối chóp tới mặt phẳng chứa đáy của khối chóp) thì thể tích V của khối chóp đó được tính theo công thức
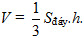
Ví dụ 2. Tính thể tích của khối tứ diện đều có cạnh bằng a.
Giải
Xem tứ diện ABCD (cạnh bằng a) như hình chóp có đỉnh là A và đáy là tam giác đều BCD có cạnh bằng a (h.27).
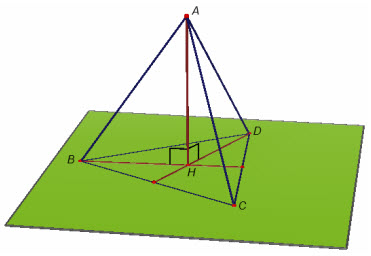
Hình 27
Diện tích mặt đáy là
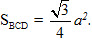
Gọi H là tâm của tam giác đều BCD thì AH là đường cao của hình chóp A.BCD. Bởi vậy chiều cao của hình chóp là
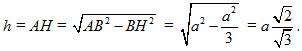
Từ đó ta suy ra khối tứ diện ABCD có thể tích là
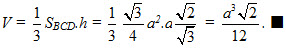
Ví dụ 3. Tính thể tích của khối tám mặt đều có cạnh bằng a.
Giải
Trên hình 28, ta có khối tám mặt đều
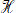
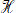
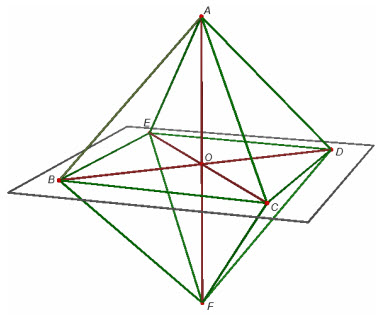
Hình 28
Chú ý rằng BCDE là hình vuông cạnh a với tân O và tam giác ABD là tam giác vuông cân đỉnh A, ta tính được :
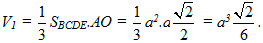
Từ đó suy ra khối tám mặt đều nói trên có thể tích là
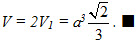
4. Thể tích của khối lăng trụ
Bài toán. Tính thể tích V của khối lăng trụ ABC.A[SUP]’[/SUP]B[SUP]’[/SUP]C[SUP]’[/SUP] biết diện tích đáy ABC bằng S và chiều cao (khoảng cách giữa hai mặt phẳng chứa hai đáy) bằng h (h.29).
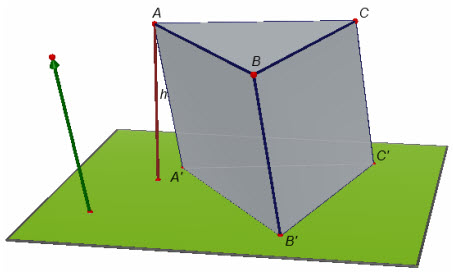
Hình 29
2(để giải bài toán)
a) Chia khối lăng trụ ABC.A[SUP]’[/SUP]B[SUP]’[/SUP]C[SUP]’[/SUP] thành bà khối tứ diện bởi các mặt phẳng (A[SUP]’[/SUP]BC[SUP]’[/SUP]) và (A[SUP]’[/SUP]BC), hãy kể tên ba khối tứ diện đó.
b) Chứng tỏ rằng ba khối tứ diện đó có thể tích bằng nhau.
c) Từ đó suy ra công thức V = S.h. Hãy phát biểu bằng lời công thức đó.
Bây giờ, xét khối lăng trụ có đáy là một đa giác bất kì. Vì bất kì đa giác nào cũng có thể phân chia được thành các tam giác không có điểm trong chung nên có thể phân chia khối lăng trụ đó thành các khối lăng trụ tam giác có cùng chiều cao (h.30). Tổng các thể tích của chúng chính là thể tích của khối lăng trụ ban đầu. Từ đó suy ra định lí sau đây.
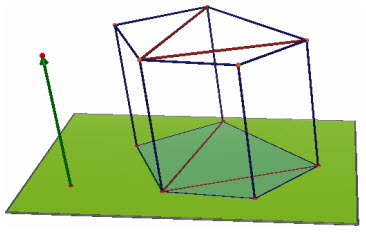
Hình 30
ĐỊNH LÍ 3
Thể tích của khối lăng trụ bằng tích số của diện tích mặt đáy và chiều cao của khối lăng trụ đó.
Ví dụ 4. Cho khối lăng trụ ABC.A[SUP]’[/SUP]B[SUP]’[/SUP]C[SUP]’[/SUP]. Gọi M, N lần lượt là trung điểm của hai cạnh AA[SUP]’[/SUP] và BB[SUP]’[/SUP]. Mặt phẳng (MNC[SUP]’[/SUP]) chia khối lăng trụ đã cho thành hai phần. Tính tỉ số thể tích của hai phần đó.
Giải
Nếu gọi V là thể tích của khối lăng trụ thì thể tích của khối tứ diện C[SUP]’[/SUP]ABC là
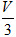


Và thể tích khối đa diện ABCMNC[SUP]’[/SUP] là
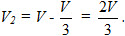
Ta có tỉ số thể tích hai phần được phân chia là
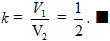
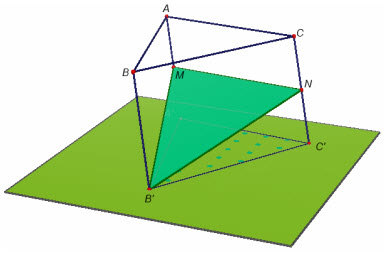
Hình 31
Câu hỏi và bài tập
15. Cho tam giác ABC cố định và một điểm S thay đổi. Thể tích của khối chóp S.ABC có thay đổi hay không nếu :
a) Đỉnh S di chuyển trên một mặt phẳng song song với mặt phẳng (ABC) ;
b) Đỉnh S di chuyển trên một mặt phẳng song song với chỉ một cạnh đáy ;
c) Đỉnh S di chuyển trên một mặt phẳng song song với một cạnh đáy ;
16. Hãy chia một khối tứ diện thành hai khối tứ diện sao cho tỉ số thể tích của hai khối tứ diện này bằng một số k > 0 cho trước.
17. Tính thể tích của khối hộp ABCD.A[SUP]’[/SUP]B[SUP]’[/SUP]C[SUP]’[/SUP]D[SUP]’[/SUP], biết rằng AA[SUP]’[/SUP]B[SUP]’[/SUP]D[SUP]’[/SUP] là khối tứ diện đều cạnh a.
18. Tính thể tích của khối lăng trụ n-giác đều có tất cả các cạnh đều bằng a.
19. Cho khối lăng trụ đứng ABC.A[SUP]’[/SUP]B[SUP]’[/SUP]C[SUP]’[/SUP] có đáy là tam giác ABC vuông tại A, AC = b,
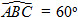
a) Tính độ dài đoạn thẳng AC[SUP]’[/SUP].
b) Tính thể tích khối lăng trụ đã cho.
20. Cho khối lăng trụ tam giác ABC.A[SUP]’[/SUP]B[SUP]’[/SUP]C[SUP]’[/SUP] có đáy là tam giác đều cạnh a, điểm A[SUP]’[/SUP] cách đều ba điểm A, B, C, cạnh bên AA[SUP]’[/SUP] tạo với mặt phẳng đáy một góc 60[SUP]o[/SUP].
a) Tính thể tích của khối lăng trụ đó.
b) Chứng minh rằng mặt bên BCC[SUP]’[/SUP]B[SUP]’[/SUP] là một hình chữ nhật.
c) Tính tổng diện tích các mặt bên của hình lăng trụ ABC.A[SUP]’[/SUP]B[SUP]’[/SUP]C[SUP]’[/SUP] (tổng đó gọi là diện tích xung quanh của hình (hoặc khối) lăng trụ đã cho).
21. Cho điểm M nằm trong hình tứ diện đều ABCD. Chứng minh rằng tổng các khoảng cách từ M tới bốn mặt của tứ diện là một số không phụ thuộc vào vị trí của điểm M. Tổng đó bằng bao nhiêu nếu cạnh của tứ diện đều bằng a ?
22. Cho khối lăng trụ tam giác đều ABC.A[SUP]’[/SUP]B[SUP]’[/SUP]C[SUP]’[/SUP]. Gọi M là trung điểm của AA[SUP]’[/SUP] . Mặt phẳng đi qua M, B[SUP]’[/SUP], C chia khối lăng trụ thành hai phần. Tính tỉ số thể tích của hai phần đó.
23. Cho khối chóp tam giác S.ABC. Trên ba đường thẳng SA, SB, SC lần lượt lấy ba điểm A[SUP]’[/SUP], B[SUP]’[/SUP], C[SUP]’[/SUP] khác với S. Gọi V và V[SUP]’[/SUP] lần lượt là thể tích của các khối chóp S.ABC và S.A[SUP]’[/SUP]B[SUP]’[/SUP]C[SUP]’[/SUP]. Chứng minh rằng :
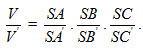
24. Khối chóp S.ABCD có đáy là hình bình hành, M là trung điểm của cạnh SC. Mặt phẳng (P) đi qua AM, song song với BD chia khối chóp thành hai phần. Tính tỉ số thể tích của hai phần đó.
25. Chứng minh rằng nếu có phép vị tự tỉ số k biến tứ diện ABCD thành tứ diện A[SUP]’[/SUP]B[SUP]’[/SUP]C[SUP]’[/SUP]D[SUP]’[/SUP] thì
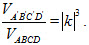
NGUỒN: SƯU TẦM
