Toán 12 - Chương II - Bài 2. Khái niệm về mặt tròn xoay
Mặt cầu là một trường hợp đơn giản của các mặt tròn xoay mà ta sẽ nói đến trong mục này.
Trước hết, ta định nghĩa trục của đường tròn : Trục của đường tròn (O ; R) là đường thẳng đi qua O và vuông góc với mặt phẳng chưa đường tròn đó.
Dễ thấy rằng khi điểm M không nằm trên đường thẳng
 thì có một đường tròn duy nhất đi qua M và có trục là
thì có một đường tròn duy nhất đi qua M và có trục là
 , kí hiệu đường tròn đó là
, kí hiệu đường tròn đó là
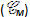 (h.37).
(h.37).
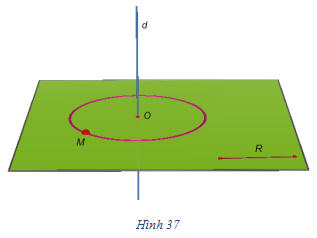
?1 Đường tròn
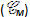 được xác định như thế nào ?
được xác định như thế nào ?
Trong trường hợp điểm M nằm trên
 , ta quy ước “đường tròn”
, ta quy ước “đường tròn”
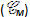 chỉ gồm duy nhất điểm M.
chỉ gồm duy nhất điểm M.
1. Định nghĩa
Trong không gian, cho hình H và đường thẳng
 . Hình gồm tất cả các đường tròn
. Hình gồm tất cả các đường tròn
 với M thuộc H được gọi là hình tròn xoay sinh bởi Hkhi quay quanh
với M thuộc H được gọi là hình tròn xoay sinh bởi Hkhi quay quanh
 . Đường thẳng
. Đường thẳng
 gọi là trục của hình tròn xoay đó.
gọi là trục của hình tròn xoay đó.
Khi hìnhH là một đường thì hình tròn xoay sinh bởi nó còn gọi là mặt tròn xoay.

Lọ hoa ở hình 38 cho ta hình ảnh của một mặt tròn xoay. Mặt tròn xoay đó sinh bởi đường (L) khi quay quanh đường thẳng
 .
.
Nói chung, các đồ gốm nếu được chế tạo bằng cách dùng bàn xoay đều có dạng là các mặt tròn xoay.
2. Một số ví dụ
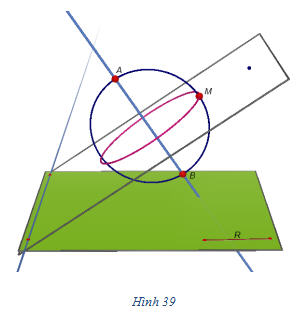
Ví dụ 1. Nếu hình [SUB]H[/SUB] là đường tròn có đường kính AB nằm trên đường thẳng
 thì rõ ràng hình tròn xoay sinh bởi H khi quay quanh
thì rõ ràng hình tròn xoay sinh bởi H khi quay quanh
 là mặt cầu đường kính AB (h.39).
là mặt cầu đường kính AB (h.39).
Nếu H là đường tròn có đường kính AB nằm trên đường thẳng
 thì hình tròn xoay sinh bởi H khi quay quanh
thì hình tròn xoay sinh bởi H khi quay quanh
 là khối cầu đường kính AB (h.39).
là khối cầu đường kính AB (h.39).
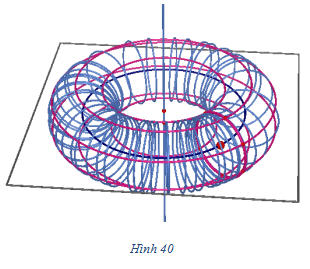
Ta xét trường hợp [SUB]H[/SUB] là đường tròn nằm trong cùng một mặt phẳng với đường thẳng
 nhưng không cắt
nhưng không cắt
 . Hình tròn xoay sinh bởi đường tròn đó khi quay quanh
. Hình tròn xoay sinh bởi đường tròn đó khi quay quanh
 được gọi là mặt xuyến (h.40)
được gọi là mặt xuyến (h.40)
Ví dụ 2. Cho 2 đường thẳng
 và l chéo nhau. Xét hình tròn xoay sinh bởi đường thẳng l khi quay quanh đường thẳng
và l chéo nhau. Xét hình tròn xoay sinh bởi đường thẳng l khi quay quanh đường thẳng
 .
.
Gọi PQ là đường vuông góc chung của 2 đường thẳng
 và l (P
và l (P
 l, Q
l, Q

 ) (h.41). Khi đó, các đường tròn
) (h.41). Khi đó, các đường tròn
 càng lớn khi M thuộc l càng cách xa điểm P và
càng lớn khi M thuộc l càng cách xa điểm P và
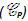 là đường tròn có bán kính bé nhất (bằng PQ).
là đường tròn có bán kính bé nhất (bằng PQ).
Trong trường hợp này, hình tròn xoay nhận được gọi là mặt hypeboloit tròn xoay một tầng. (Sở dĩ có tên gọi này là vì mặt tròn xoay đó có thể sinh bởi một hypebol khi quay quanh trục ảo của nó).

Trong các §3 và §4, chúng ta sẽ xét hình tròn xoay sinh bởi đường thẳng l khi quay quanh đường thẳng
 trong trường hợp hai đường thẳng đó cùng nằm trong một mặt phẳng.
trong trường hợp hai đường thẳng đó cùng nằm trong một mặt phẳng.
NGUỒN: SƯU TẦM
Dễ thấy rằng khi điểm M không nằm trên đường thẳng


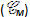

?1 Đường tròn
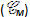
Trong trường hợp điểm M nằm trên

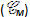
1. Định nghĩa
Trong không gian, cho hình H và đường thẳng

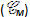


Khi hìnhH là một đường thì hình tròn xoay sinh bởi nó còn gọi là mặt tròn xoay.

Lọ hoa ở hình 38 cho ta hình ảnh của một mặt tròn xoay. Mặt tròn xoay đó sinh bởi đường (L) khi quay quanh đường thẳng

Nói chung, các đồ gốm nếu được chế tạo bằng cách dùng bàn xoay đều có dạng là các mặt tròn xoay.
2. Một số ví dụ
Ví dụ 1. Nếu hình [SUB]H[/SUB] là đường tròn có đường kính AB nằm trên đường thẳng


Nếu H là đường tròn có đường kính AB nằm trên đường thẳng



Ta xét trường hợp [SUB]H[/SUB] là đường tròn nằm trong cùng một mặt phẳng với đường thẳng




Ví dụ 2. Cho 2 đường thẳng


Gọi PQ là đường vuông góc chung của 2 đường thẳng




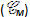
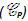
Trong trường hợp này, hình tròn xoay nhận được gọi là mặt hypeboloit tròn xoay một tầng. (Sở dĩ có tên gọi này là vì mặt tròn xoay đó có thể sinh bởi một hypebol khi quay quanh trục ảo của nó).

Trong các §3 và §4, chúng ta sẽ xét hình tròn xoay sinh bởi đường thẳng l khi quay quanh đường thẳng

NGUỒN: SƯU TẦM
