Hình 10: Bài 7: Đường Parabol

[Thandieu2]

Toán 10 - Chương III - Bài 7. Đường Parabol
​

Trong thực tế ta cũng thường gặp đường parabol, chẳng hạn:
- Đồ thị của hàm số y = ax[SUP]2[/SUP] + bx + c (với a ≠ 0) là một đường parabol;
- Các tia nước phun ra từ vòi phun nước (thường gặp ở các vườn hoa hay khi tưới cây) là những đường parabol;
- Đường đi của viên đạn đại bác là một đường parabol.


1. Định nghĩa đường parabol

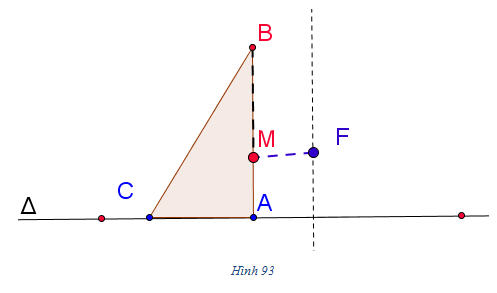
Cho một điểm F cố định và một đường thẳng

cố định không đi qua F. Tập hợp các điểm M cách đều F và

được gọi là đường parabol(hay parabol) (h. 92).
Điểm F được gọi là tiêu điểm của parabol.
Đường thẳng

được gọi là đường chuẩn của parabol.
Khoảng cách từ F đến

được gọi là tham số tiêu của parabol.

​

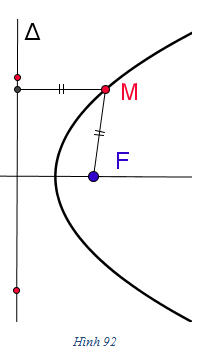
Ta có thể vẽ parabol với tiêu điểm F và đường chuẩn

như sau (h. 93) : Lấy một êke ABC (vuông ở A) và một đoạn dây không đàn hồi, có độ dài bằng AB. Đính một đầu dây vào điểm F, đầu kia vào đỉnh B của êke. Đặt êke sao cho cạnh AC nằm trên

, lấy đầu bút chì ép sát sợi dây rồi cho cạnh AC của êke trượt trên

. Khi đó đầu M của bút chì sẽ vạch nên một phần của parabol (vì ta luôn có MF = MA).

​

2. Phương trình chính tắc của parabol

Cho parabol với tiêu điểm F của đường chuẩn

.
Kẻ FP vuông góc với

. Đặt FP = p (tham số tiêu). Ta chọn hệ trục tọa độ Oxy sao cho O là trung điểm của FP và điểm F nằm trên tia Ox (h. 94).

​

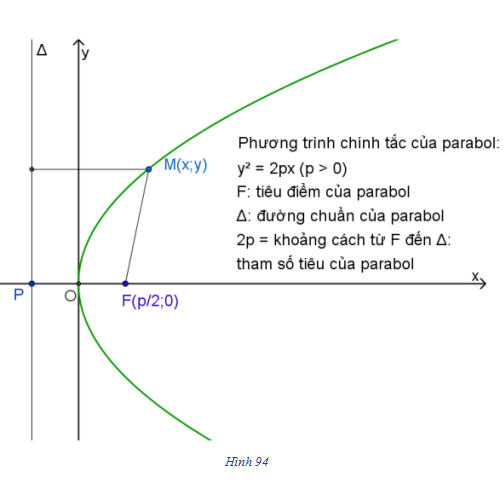
Như vậy ta có:

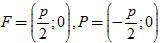
Và phương trình của đường thẳng

là

. Điểm M(x ; y) nằm trên parabol đã cho khi và chỉ khi khoảng cách MF bằng khoảng cách từ M tới

, tức là

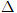
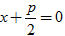
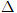
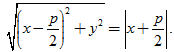
Bình phương hai vế của đẳng thức đó rồi rút gọn, ta được

Phương trình (1) gọi là phương trình chính tắc của parabol.

Từ phương trình chính tắc của parabol, hãy chứng tỏ những tính chất sau đây của parabol
a) Parabol nằm về bên phải của trục tung.
b) Ox là trục đối xứng của parabol.
c) Parabol cắt trục Ox tại điểm O và đó cũng là điểm duy nhất của Oy thuộc parabol. Gốc tọa độ O được gọi là đỉnh của parabol.

Ví dụ. Viết phương trình chính tắc của parabol đi qua điểm M(2 ; 5).
Giải. Phương trình chính tắc của parabol có dạng y[SUP]2[/SUP] = 2px. Thay tọa độ của M vào phương trình ta được 25 = 2.p.2.
Suy ra .

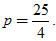
Từ đó ta được phương trình chính tắc của parabol đã cho là

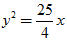
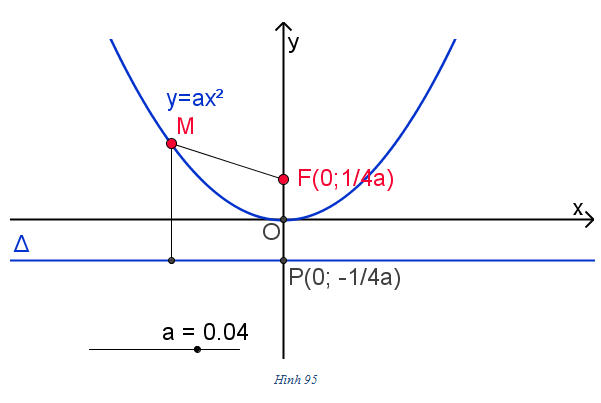
Ở môn Đại số, chúng ta đã gọi đồ thị của hàm số bậc hai y = ax[SUP]2[/SUP] + bx + c là một đường parabol.
Sở dĩ ta gọi như thế vì đồ thị đó cũng thỏa mãn định nghĩa của đường parabol mà ta vừa trình bày ở trên.
Chẳng hạn, đồ thị hàm số y = ax[SUP]2[/SUP] (a ≠ 0) là parabol có tiêu điểm

và đường chuẩn d (h.95)có phương trình:

​

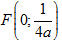
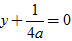
Câu hỏi và bài tập​

42. Trong các mệnh đề sau, mệnh đề nào đúng?
a) y[SUP]2[/SUP] = –2x là phương trình chính tắc của parabol.
b) y = x[SUP]2[/SUP] là phương trình chính tắc của parabol.
c) Parabol (P) : y[SUP]2[/SUP] = 2x có tiêu điểm F(0,5 ; 0) và có đường chuẩn

: x + 0,5 = 0.
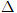
d) Parabol y[SUP]2[/SUP] = 2px (p > 0) có tiêu điểm F(p ; 0) và có đường chuẩn

: x + p = 0.

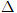
43. Viết phương trình chính tắc của parabol (P) trong mỗi trường hợp sau
a) (P) có tiêu điểm F(3 ; 0);
b) (P) đi qua điểm M(1 ; –1);
c) (P) có tham số tiêu là

.

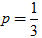
44. Cho parabol y[SUP]2[/SUP] = 2px. Tìm độ dài dây cung của parabol vuông góc với trục đối xứng tại tiêu điểm của parabol (dây cung của parabol là đoạn thẳng nối hai điểm của parabol).
45. Cho dây cung AB đi qua tiêu điểm của parabol (P). Chứng minh rằng khoảng cách từ trung điểm I của dây AB đến đường chuẩn của (P) bằng

. Từ đó có nhận xét gì về đường tròn đường kính AB ?

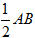
46. Trong mặt phẳng tọa độ Oxy cho điểm F(1 ; –2). Tìm hệ thức giữa x, y để điểm M(x ; y) cách đều điểm F và trục hoành.

NGUỒN: SƯU TẦM