Toán 10- Nâng Cao - Chương 3 - BÀI 5. ĐƯỜNG ELIP[/TD]
BÀI 5. ĐƯỜNG ELIP
Đường elip là một đường quen thuộc với chúng ta và thường gặp trong thực tế, chẳng hạn:
- Bóng của một đường tròn in trên mặt đất bằng phẳng dưới áng sáng mặt trời thường là một đường elip.
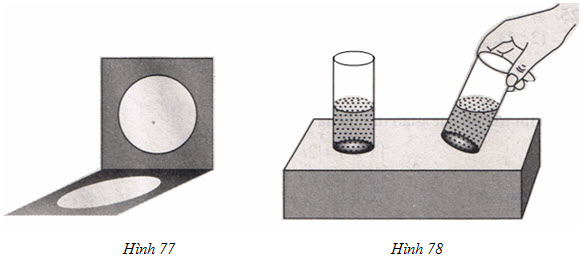
- Ta đổ một ít nước màu vào một cốc thủy tinh hình trụ. Nết đặt đứng cốc nước trên mặt bàn nằm ngang thì mặt thoáng của nước trong cốc là một hình tròn, giới hạn bởi một đường tròn. Nếu ta nghiêng cốc nước đi thì mặt thoáng của nước được giới hạn bởi một đường elip.
- Quỹ đạo của Trái Đất khi quay quanh Mặt Trời là một đường elip. Các nhà thiên văn học đã phát hiện ra rằng, trong hệ Mặt Trời, mỗi hành tinh đều chuyển động theo một quỹ đạo là đường elip (h. 79).
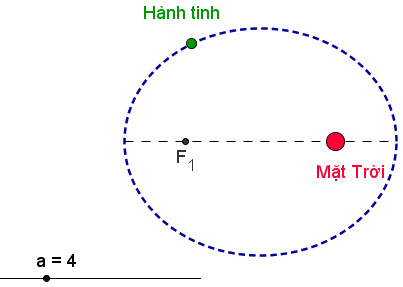
Hình 79
1. Định nghĩa đường elip

Em hãy đóng lên mặt một bảng gỗ hai chiếc đinh tại hai điểm F[SUB]1[/SUB] và F[SUB]2[/SUB] (h. 80).
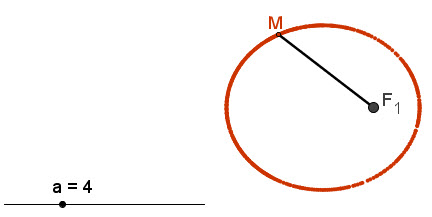
Hình 80
Lấy một vòng dây kín không đàn hồi, có độ dài lớn hơn hai lần khoảng cách F[SUB]1[/SUB]F[SUB]2[/SUB]. Quàng sợi dây vào hai chiếc đinh, đặt đầu bút chì vào trong vòng dây rồi căng ra để vòng dây trở thành một tam giác. Hãy di chuyển đầu bút chì sao cho dây luôn luôn căng và áp sát mặt gỗ. Khi đó đầu bút chì sẽ vạch ra một đường mà ta gọi là đường elip.
?1. Trong cách vẽ đường elip ở trên, gọi vị trí đầu bút chì là M. Khi M thay đổi, có nhận xét gì về chi vi tam giác M F[SUB]1[/SUB]F[SUB]2[/SUB], và về tổng MF[SUB]1[/SUB] +MF[SUB]2[/SUB] ?
ĐỊNH NGHĨA
Cho hai điểm cố định F[SUB]1[/SUB] và F[SUB]2[/SUB], với F[SUB]1[/SUB]F[SUB]2[/SUB] = 2c (c > 0).
Đường elip (còn gọi là elip) là tập hợp các điểm M sao cho MF[SUB]1[/SUB] + MF[SUB]2[/SUB] = 2a, trong đó a là số cho trước lớn hơn c.
Hai điểm F[SUB]1[/SUB] và F[SUB]2[/SUB] gọi là các tiêu điểm của elip. Khoảng cách 2c được gọi là tiêu cự của elip.
2. Phương trình chính tắc của elip
Cho elip (E) như trong định nghĩa trên. Ta chọn hệ trục tọa độ Oxy có gốc là trung điểm của đoạn thẳng F[SUB]1[/SUB]F[SUB]2[/SUB]. Trục Oy là đường trung trực của F[SUB]1[/SUB]F[SUB]2[/SUB] và [SUB]2[/SUB] nằm trên tia Ox (h. 81).
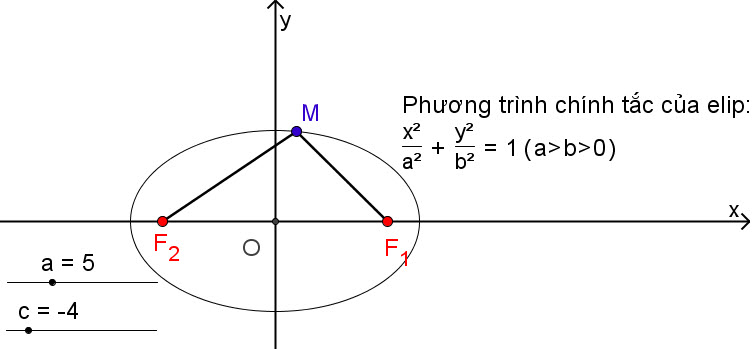
Hình 81
?2. Với cách chọn hệ trục tọa độ như vậy, hãy cho biết tọa độ của hai tiêu điểm F[SUB]1[/SUB] và F[SUB]2[/SUB].

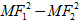

Các đoạn thẳng MF[SUB]1[/SUB], MF[SUB]2[/SUB] được gọi là bán kính qua tiêu của điểm M.
Bây giờ ta lập phương trình của elip (E) đối với hệ trục tọa độ đã chọn như trên.
Ta có
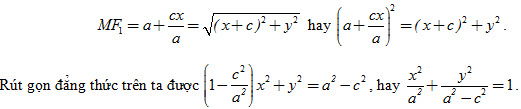
Vì a[SUP]2[/SUP] + c[SUP]2[/SUP] > 0 nên ta có thể đặt a[SUP]2[/SUP] – c[SUP]2[/SUP] = b[SUP]2[/SUP] (với b > 0) và được
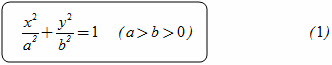
Ngược lại, có thể chứng minh được rằng : Nếu điểm M có tọa độ (x ; y) thỏa mãn (1) thì
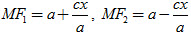
Phương trình (1) gọi là phương trình chính tắc của elip đã cho.
Ví dụ 1. Cho ba điểm
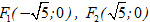
a) Hãy viết phương trình chính tắc của elip có tiêu điểm là F[SUB]1[/SUB], F[SUB]2[/SUB] và đi qua I.
b) Khi M chạy trên elip đó, khoảng cách MF[SUB]1[/SUB] có giá trị nhỏ nhất và giá trị lớn nhất bằng bao nhiêu?
Giải.
a) Elip có phương trình chính tắc
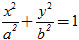
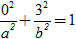
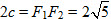
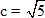
Vậy elip cần tìm có phương trình chính tắc là
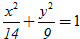
b) Theo công thức về độ dài bán kính qua tiêu, ta có
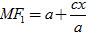
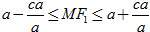

Ví dụ 2. Viết phương trình chính tắc của elip đi qua hai điểm M(0 ; 1) và
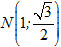
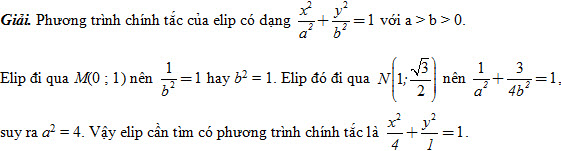
Ta có c[SUP]2[/SUP] = a[SUP]2[/SUP] – b[SUP]2[/SUP] = 4 – 1 = 3. Vậy tọa độ các tiêu điểm của elip đó là
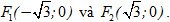
3. Hình dạng của elip
a) Tính đối xứng của elip
?3 Cho elip có phương trình (1) và một điểm M(x[SUB]0[/SUB] ; y[SUB]0[/SUB]) nằm trên elip. Hỏi các điểm sau đây có nằm trên elip không?
M[SUB]1[/SUB] (–x[SUB]0[/SUB] ; y[SUB]0[/SUB]), M[SUB]2[/SUB] (x[SUB]0[/SUB] ; –y[SUB]0[/SUB]), M[SUB]3[/SUB] (–x[SUB]0[/SUB] ; –y[SUB]0[/SUB])
Từ đó suy ra
Elip có phương trình (1) nhận các trục tọa độ làm các trục đối xứng và gốc tọa độ làm tâm đối xứng.
b) Hình chữ nhật cơ sở
Elip với phương trình chính tắc (1), cắt trục Ox tại hai điểm A[SUB]1[/SUB] và A[SUB]2[/SUB], cắt trục Oy tại hai điểm B[SUB]1[/SUB] và B[SUB]2[/SUB]. Bốn điểm đó gọi là các đỉnh của elip. Trục Ox được gọi là trục lớn, trục Oy được gọi là trục bé (hay trục nhỏ). Người ta cũng gọi đoạn A[SUB]1[/SUB]A[SUB]2[/SUB] là trục lớn, đoạn B[SUB]1[/SUB]B[SUB]2[/SUB] là trục bé. Độ dài trục lớn là 2a, độ dài trục bé là 2b.
Vẽ qua A[SUB]1[/SUB] và A[SUB]2[/SUB] hai đường thẳng song song với trục tung, vẽ qua B[SUB]1[/SUB] và B[SUB]2[/SUB] hai đường thẳng song song với trục hoành. Bốn đường thẳng đó tạo thành hình chữ nhật PQRS. Ta gọi hình chữ nhật đó là hình chữ nhật cơ sở của elip (h. 82).
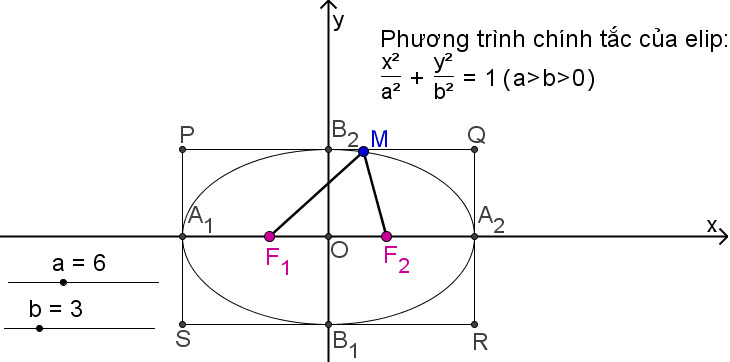
Hình 82
?4 Nếu xét điểm M(x ; y) nằm trên elip có phương trình chính tắc (1) thì giá trị nhỏ nhất và lớn nhất của x là bao nhiêu? Giá trị nhỏ nhất và lớn nhất của y là bao nhiêu?
Từ đó suy ra
Mọi điểm của elip nếu không phải là đỉnh đều nằm trong hình chữ nhật cơ sở của nó. Bốn đỉnh của elip là trung điểm các cạnh của hình chữ nhật cơ sở.
c) Tâm sai của elip
Tỉ số giữa tiêu cự và độ dài trục lớn của elip gọi là tâm sai của elip và được kí hiệu là e, tức là
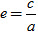
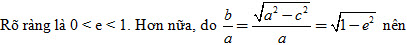
- Nếu tâm sai e càng bé (tức là càng gần 0) thì b càng gần a và hình chữ nhật cơ sở càng gần với hình vuông, do đó đường elip càng “béo”;
- Nếu tâm sai e càng lớn (tức là càng gần 1) thì tỉ số
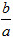
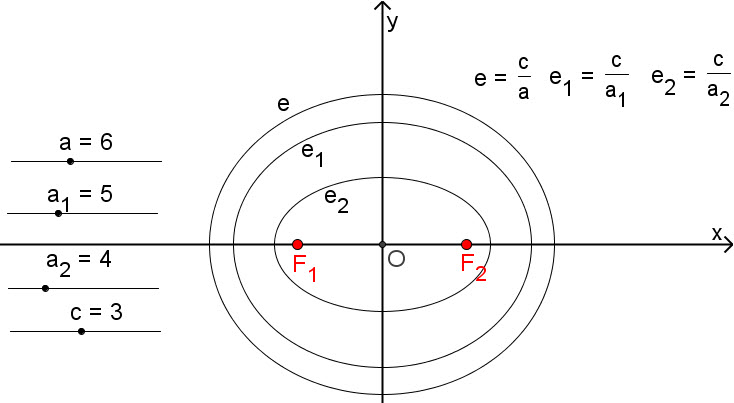
Hình 83
Ví dụ 3. Một đường hầm xuyên qua núi có chiều rộng là 20 m, mặt cắt đứng của đường hầm có dạng nửa elip như hình 84. Biết rằng tâm sai của đường elip là e ≈ 0,5. Hãy tìm chiều cao của đường hầm đó.
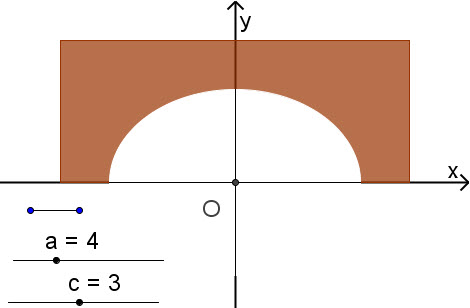
Hình 84
Giải. Gọi chiều cao của đường hầm là b. Nửa trục lớn của elip là a = 10m. Elip có nửa tiêu cự là c = a.e ≈ 5 (m).
Chiều cao của hầm là
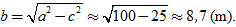
d) Elip và phép co đường tròn
Bài toán. Trong mặt phẳng tọa độ, chho đường tròn (C ) có phương trình x[SUP]2[/SUP] + y[SUP]2[/SUP] = a[SUP]2[/SUP] và một số k (0 < k < 1). Với mỗi điểm M(x ; y) trên (C ), lấy điểm M’(x’ ; y’) sao cho x’ = x và y’ = ky. Tìm tập hợp các điểm M’.
Giải. Từ x’ = x, y’ = ky suy ra x’ = x,
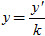
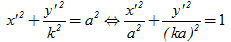
Đặt b = ka, ta được tập hợp các điểm M’ là elip (E) có phương trình chính tắc
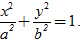
Người ta nói: Phép co về trục hoành theo hệ số k bến đường tròn (C ) thành elip (E).
Hình 85
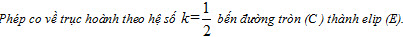

Nhà thiên văn học người Đức Kê-ple (J. Kepler) đã chứng minh rằng: Mỗi hành tinh trong hệ Mặt Trời đều chuyển động theo quỹ đạo là một đường elip mà tâm Mặt Trời là một tiêu điểm

Johannes Kepler (1571 - 1630)
Tâm sai của các quỹ đạo của 8 hành tinh đã quen thuộc trong hệ Mặt Trời như sau:
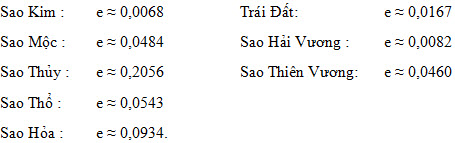
Trong các hành tinh trên thì Sao Kim, Trái Đất và Sao Hải Vương có quỹ đạo gần giống đường tròn hơn.
Ngoài ra, chúng ta cũng biết rằng Mặt Trăng quay quanh Trái Đất theo quỹ đạo là một đường elip mà tâm Trái Đất là một tiêu điểm. Tâm sai của quỹ đạo này là e ≈ 0,0549.
Câu hỏi và bài tập
30. Cho elip (E) có phương trình chính tắc
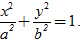
a) Tiêu cự của (E) là 2c, trong đó c[SUP]2[/SUP] = a[SUP]2[/SUP] – b[SUP]2[/SUP].
b) (E) có độ dài là trục lớn bằng 2a, độ dài trục bé bằng 2b.
c) (E) có tâm sai
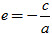
d) Tọa độ các tiêu điểm của (E) là F[SUB]1[/SUB] = (–c ; 0), F[SUB]2[/SUB] = (c ; 0).
e) Điểm (b ; 0) là một đỉnh của (E).
31. Tìm tọa độ các tiêu điểm, các đỉnh, độ dài trục lớn, độ dài trục bé của mỗi elip có phương trình sau
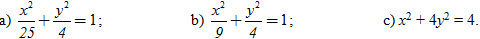
32. Viết phương trình chính tắc của đường elip (E) trong mỗi trường hợp sau
a) (E) có độ dài trục lớn bằng 8 và tâm sai
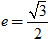
b) (E) có độ dài trục bé bằng 8 và tiêu cự bằng 4;

a) Tính độ dài dây cung của (E) đi qua một tiêu điểm và vuông góc với trục tiêu (đoạn thẳng nối hai điểm của elip gọi là dây cung của elip, trục chứa các tiêu điểm gọi là trục tiêu của elip).
b) Tìm trên (E) điểm M sao cho MF[SUB]1[/SUB] = 2MF[SUB]2[/SUB], trong đó F[SUB]1[/SUB], F[SUB]2[/SUB] lần lượt là các tiêu điểm của (E) nằm bên trái và bên phải trục tung.
34. Vệ tinh nhân tạo đầu tiên được Liên Xô (cũ) phóng từ Trái Đất năm 1957. Quỹ đạo của vệ tinh đó là một đường elip nhận tâm của Trái Đất là một tiêu điểm. Người ta đo được vệ tinh cách bề mặt Trái Đất gần nhất là 583 dặm và xa nhất là 1342 dặm (1 dặm ≈ 1,609 km). Tìm tâm sai của quỹ đạo đó biết bán kính của Trái Đất xấp xỉ 4000 dặm.
35. Trong mặt phẳng tọa độ Oxy, cho điểm A chạy trên trục Ox, điểm B chạy trên trục Oy nhưng độ dài đoạn AB bằng a không đổi. Tìm tập hợp các điểm M thuộc đoạn AB sao cho MB = 2MA.
SƯU TẦM
