Toán 10 - Chương III - Bài 4. Đường tròn
1. Phương trình đường tròn
Trên mặt phẳng tọa độ, cho đường tròn (C ) có tâm I(x[SUB]0[/SUB] ; y[SUB]0[/SUB]) và bán kính R (h. 75).
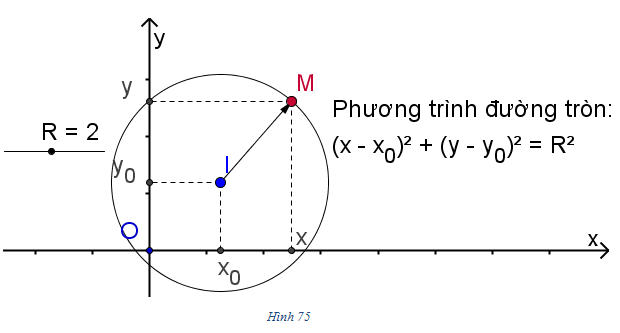
Điểm M(x ; y) thuộc đường tròn (C ) khi và chỉ khi IM = R, hay là

Ta gọi phương trình (1) là phương trình của đường tròn (C ).

a) Hãy viết phương trình đường tròn tâm P và đi qua Q.
b) Hãy viết phương trình đường tròn đường kính PQ.
2. Nhận dạng phương trình đường tròn
Biến đổi phương trình (1) về dạng
x[SUP]2[/SUP] + y[SUP]2[/SUP] - 2x[SUB]0[/SUB]x - 2y[SUB]0[/SUB]y + x[SUB]0[/SUB][SUP]2[/SUP] + y[SUB]0[/SUB][SUP]2[/SUP] - R[SUP]2[/SUP] = 0,
Ta thấy mỗi đường tròn trong mặt phẳng tọa độ đều có phương trình dạng
x[SUP]2[/SUP] + y[SUP]2[/SUP] + 2ax + 2by + c = 0 (2)
Ngược lại, phải chăng mỗi phương trình dạng (2) với a, b, c tùy ý, đều là phương trình của một đường tròn?
Ta biến đổi phương trình (2) về dạng
(x + a)[SUP]2[/SUP] + (y + b)[SUP]2[/SUP] = a[SUP]2[/SUP] + b[SUP]2[/SUP] - c.
Nếu gọi I là điểm có tọa độ (-a ; -b), còn (x ; y) là tọa độ của điểm M thì vế trái của đẳng thức trên chính là IM[SUP]2[/SUP]. Bởi vậy ta đi đến kết luận
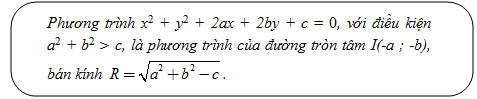

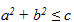
? Trong các phương trình sau, phương trình nào là phương trình đường tròn ?
a)3x[SUP]2[/SUP] + 3y[SUP]2[/SUP] + 2003x - 17y = 0;
b)x[SUP]2[/SUP] + y[SUP]2[/SUP] - 2x - 6y + 103 = 0;
c)x[SUP]2[/SUP] + 2y[SUP]2[/SUP] - 2x + 5y + 2 = 0;
d)x[SUP]2[/SUP] + y[SUP]2[/SUP] - 2xy + 3x - 5y - 1 = 0.
Ví dụ. Viết phương trình đường tròn đi qua ba điểm M(1 ; 2), N(5 ; 2) và P(1 ; -3).
Giải. Gọi I(x ; y) và R là tâm và bán kính của đường tròn đi qua ba điểm M, N, P.
Từ điều kiện IM = IN = IP ta có hệ phương trình
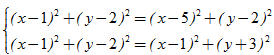
Dễ dàng tìm được nghiệm của hệ là x = 3 ; y = –0,5. Vậy I = (3 ; –0,5).
Khi đó R[SUP]2[/SUP] = IM[SUP]2[/SUP]= 10,25. Phương trình đường tròn cần tìm là
(x - 3)[SUP]2[/SUP] + (y + 0,5)[SUP]2[/SUP] = 10,25.
Có thể giải bài toán bằng cách khác.
Giả sử phương trình đường tròn có dạng
x[SUP]2[/SUP] + y[SUP]2[/SUP] + 2ax + 2by + c = 0.
Do M, N, P thuộc đường tròn nên ta có hệ phương trình với ba ẩn số a, b, c
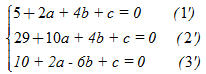
Từ (1’) và (2’) suy ra 24 + 8a = 0, do đó a = -3. Từ (1’) và (3’) suy ra -5 + 10b = 0, do đó b = 0,5. Thay a và b vừa tìm được vào (1’) ta có
c = –5 + 6 – 2 = c1.
Vậy phương trình đường tròn cần tìm là x[SUP]2[/SUP] + y[SUP]2[/SUP] – 6x + y – 1 = 0.
3. Phương trình tiếp tuyến của đường tròn
Bài toán 1. Viết phương trình tiếp tuyến của đường tròn
(C) : (x + 1)[SUP]2[/SUP] + (y - 2)[SUP]2[/SUP] = 5,
Biết rằng tiếp tuyến đó đi qua điểm
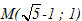
Giải. Đường tròn (C ) có tâm I(-1 ; 2) và bán kính
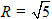
Đường thẳng
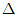
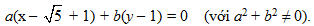
Khoảng cách từ I(-1 ; 2) tới đường thẳng
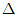
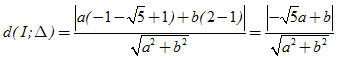
Để
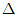
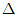
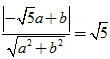
Hay :
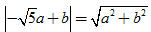
Từ đó:
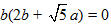
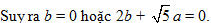
Nếu b = 0, ta có thể chọn a = 1 và được tiếp tuyến
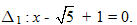
Nếu
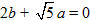
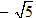
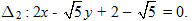
Để viết phương trình tiếp tuyến của đường tròn, ta thường dùng điều kiện sau
Đường thẳng tiếp xúc với đường tròn khi và chỉ khi khoảng cách từ tâm đường tròn đến đường thẳng bằng bán kính của đường tròn.
Tuy nhiên, để viết phương trình tiếp tuyến của đường tròn tại điểm M cho trước thuộc đường tròn, ta có cách giải đơn giản hơn.
Bài toán 2. Cho đường tròn
x[SUP]2[/SUP] + y[SUP]2[/SUP] – 2x + 4y – 20 = 0 và điểm M(4 ; 2).
a) Chứng tỏ rằng điểm M nằm trên đường tròn đã cho.
b) Viết phương trình tiếp tuyến của đường tròn tại điểm M.
Giải. (h. 76)
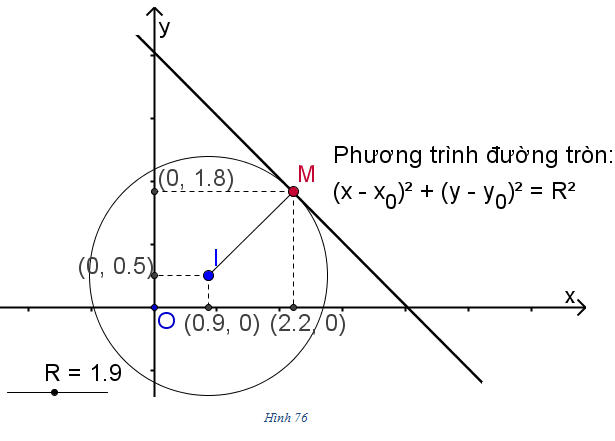
a) Thay tọa độ (4 ; 2) của M vào vế trái của phương trình đường tròn, ta được
4[SUP]2[/SUP] + 2[SUP]2[/SUP] – 2.4 + 4.2 – 20 = 0.
Vậy M nằm trên đường tròn.
b) Đường tròn có tâm I = (1 ; -2). Tiếp tuyến của đường tròn tại M là đường thẳng đi qua M và nhận
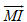
Vì
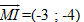
–3(x – 4) – 4(y – 2) = 0
hay 3x + 4y – 20 = 0.

(C) : x[SUP]2[/SUP] + y[SUP]2[/SUP] - 3x + y = 0.

Câu hỏi và bài tập
x[SUP]2[/SUP] + y[SUP]2[/SUP] + px + (p – 1)y = 0. (1)
Hỏi trong các mệnh đề sau, mệnh đề nào đúng ?
a) (1) là phương trình của một đường tròn.
b) (1) là phương trình của một đường tròn đi qua gốc tọa độ.
c) (1) là phương trình của một đường tròn có tâm J(p ; p – 1).
d) (1) là phương trình của đường tròn có tâm

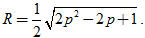
22. Viết phương trình đường tròn (C ) trong mỗi trường hợp sau
a) (C ) có tâm I(1 ; 3) và đi qua điểm A(3 ; 1);
b) (C ) có tâm I(-2 ; 0) và tiếp xúc với đường thẳng
23. Tìm tâm và bán kính của đường tròn cho bởi mỗi phương trình sau
a) x[SUP]2[/SUP] + y[SUP]2[/SUP] - 2x - 2y - 2 = 0;
b)x[SUP]2[/SUP] + y[SUP]2[/SUP] - 4x - 6y + 2 = 0;
c)2x[SUP]2[/SUP] + 2y[SUP]2[/SUP] - 5x - 4y + 1 + m[SUP]2[/SUP] = 0.
24. Viết phương trình đường tròn đi qua ba điểm M(1 ; -2), N(1 ; 2), P(5 ; 2).
25. a) Viết phương trình đường tròn tiếp xúc với hai trục tọa độ và đi qua điểm (2 ; 1).
b) Viết phương trình đường tròn đi qua hai điểm (1 ; 1), (1 ; 4) và tiếp xúc với trục Ox.
26. Tìm tọa độ các giao điểm của đường thẳng
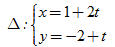
Và đường tròn (C ): (x – 1)[SUP]2[/SUP] + (y – 2)[SUP]2[/SUP] = 16.
27. Viết phương trình tiếp tuyến của đường tròn x[SUP]2[/SUP] + y[SUP]2[/SUP] = 4 trong mỗi trường hợp sau
a) Tiếp tuyến song song với đường thẳng 3x – y + 17 = 0;
b) Tiếp tuyến vuông góc với đường thẳng x + 2y – 5 = 0;
c) Tiếp tuyến đi qua điểm (2 ; -2).
28. Xét vị trí tương đối của đường thẳng
(C ) : x[SUP]2[/SUP] + y[SUP]2[/SUP] – 4x + 2y + 1 = 0.
29. Tìm tọa độ các giao điểm của hai đường tròn sau đây
(C ) : x[SUP]2[/SUP] + y[SUP]2[/SUP] + 2x + 2y – 1 = 0,
(C’ ) : x[SUP]2[/SUP] + y[SUP]2[/SUP] – 2x + 2y – 7 = 0.
SƯU TẦM
