Hình 10: Bài 3: Khoảng cách và góc

[Thandieu2]

Toán 10 - Chương III - Bài 3. Khoảng cách và góc[/TD]
​

1. Khoảng cách từ một điểm đến một đường thẳng


Bài toán 1. Trong mặt phẳng tọa độ, cho đường thẳng

có phương trình tổng quát ax + by + c = 0. Hãy tính khoảng cách d(M ;

) từ điểm M(xM ; yM) đến

.

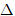
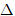
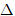
Giải. (h. 72) Gọi M′ là hình chiếu của M trên

thì độ dài đoạn M′M chính là khoảng cách từ M đến

.

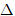
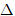
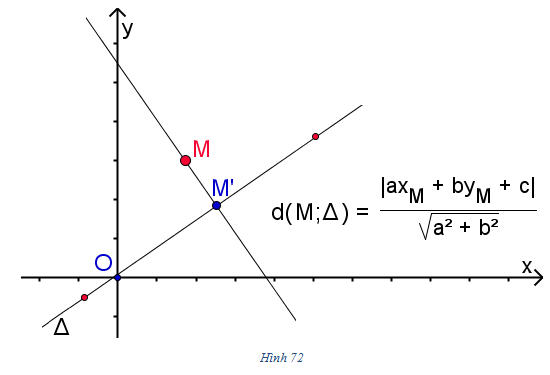
Hiển nhiên

cùng phương với vectơ pháp tuyến

của

, vậy có số k sao cho

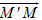
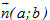
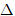
Từ đó suy ra

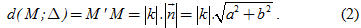
Mặt khác, nếu gọi (x′ ; y′) là tọa độ của M′ thì từ (1) ta có

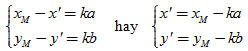
Vì M’ nằm trên

nên a(x[SUB]M[/SUB] – ka) + b(y[SUB]M[/SUB]¬ – kb) + c = 0. Từ đó suy ra:

.

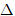
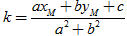
Thay giá trị của k vào (2) ta được:

1. Hãy tính khoảng cách từ điểm M đến đường thẳng

trong mỗi trường hợp sau:

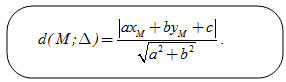
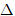
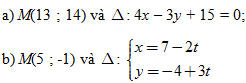
Vị trí của hai điểm đối với một đường thẳng


Cho đường thẳng

và điểm M(xM ; yM). Nếu M’ là hình chiếu (vuông góc) của M trên

thì theo lời giải của Bài toán 1, ta có

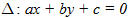
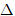
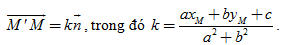
Tương tự nếu có điểm N(xN, yN) với N’ là hình chiếu của N trên

thì ta cũng có

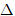
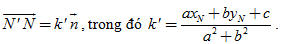
?1. Có nhận xét gì về vị trí của hai điểm M, N đối với

khi k và k’ cùng dấu ? Khi k và k’ khác dấu ?
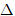
Ta có kết quả sau
Cho đường thẳng

và hai điểm M(xM ; yM), N(xN, yN) không nằm trên

. Khi đó
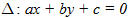
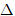
Hai điểm M, N nằm cùng phía đối với

khi và chỉ khi

2. Cho tam giác ABC có các đỉnh là A(1 ; 0), B(2 ; -3), C(-2 ; 4) và đường thẳng

. Xét xem

cắt cạnh nào của tam giác.
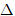
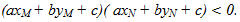
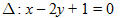
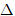
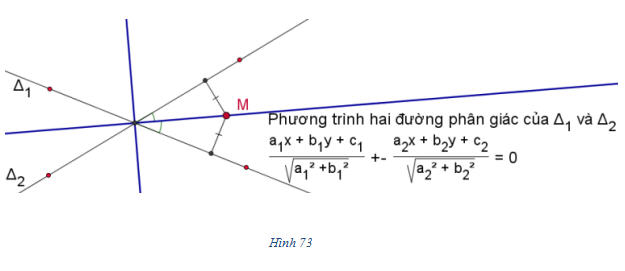
Ta có thể áp dụng công thức tính khoảng cách để viết phương trình các đường phân giác.

Bài toán 2. Cho hai đường thẳng cắt nhau, có phương trình

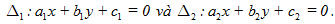
Chứng minh rằng phương trình hai đường phân giác của các góc tạo bởi hai đường thẳng đó có dạng

3. Hãy giải Bài toán 2, với chú ý rằng điểm M thuộc một trong hai đường phân giác khi và chỉ khi nó cách đều hai đường thẳng

(h. 73).

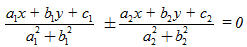
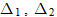
Ví dụ. Cho tam giác ABC với

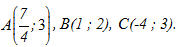
Viết phương trình đường phân giác trong của góc A.

Giải. Dễ thấy các đường thẳng AB và AC có phương trình
AB : 4x – 3y + 2 = 0 và AC : y – 3 = 0.
Các đường phân giác trong và phân giác ngoài của góc A có phương trình

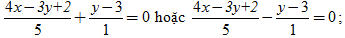
Hay:
4x + 2y – 13 = 0 (đường phân giác d[SUB]1[/SUB])
4x – 8y + 17 = 0 (đường phân giác d[SUB]2[/SUB]).
Do hai điểm B, C nằm cùng phía đối với đường phân giác ngoài và nằm khác phía đối với đường phân giác trong của góc A nên ta chỉ cần xét vị trí của B, C đối với một trong hai đường, chẳng hạn d[SUB]2[/SUB]. Thay tọa độ của B, C lần lượt vào vế trái của d[SUB]2[/SUB] ta được.
4 – 16 + 17 = 5 > 0 và –16 – 24 + 17 = –23 < 0.
Tức là B, C nằm khác phía đối với d[SUB]2[/SUB].
Vậy phương trình đường phân giác trong của góc A là

d[SUB]2[/SUB]: 4x – 8y + 17 = 0.


2. Góc giữa hai đường thẳng


ĐỊNH NGHĨA
Hai đường thẳng a và b cắt nhau tạo thành bốn góc. Số đo nhỏ nhất của các góc đó được gọi là số đo của góc giữa hai đường thẳng a và b, hay đơn giản là góc giữa a và b.
Khi a song song hoặc trùng với b, ta quy ước góc giữa chúng bằng 0[SUP]0[/SUP].
?2. Trên hình 74, góc giữa hai đường thẳng a và b bằng bao nhiêu? Hãy so sánh góc đó với góc giữa hai vectơ

và góc giữa hai vectơ

.

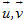
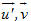
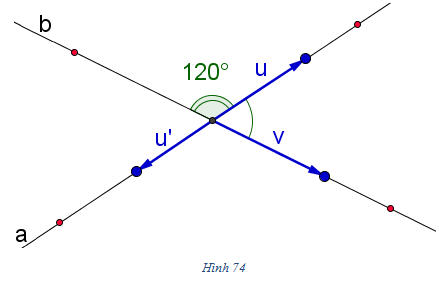
Góc giữa hai đường thẳng a và b được kí hiệu

, hay đơn giản là (a,b). Góc này không vượt quá 90[SUP]0[/SUP] nên ta có

4. Cho biết phương trình của hai đường thẳng

và

lần lượt là

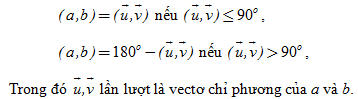
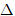
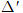
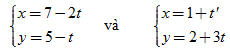
Tìm tọa độ vectơ chỉ phương của hai đường thẳng và tìm góc hợp bởi hai đường thẳng đó.

Bài toán 3
a) Tìm côsin của góc giữa hai đường thẳng

lần lượt cho bởi các phương trình
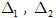
a[SUB]1[/SUB]x + b[SUB]1[/SUB]y + c[SUB]1[/SUB] = 0 và a[SUB]2[/SUB]x + b[SUB]2[/SUB]y + c[SUB]2[/SUB] = 0.
b) Tìm điều kiện để hai đường thẳng

vuông góc với nhau.
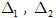
c) Tìm điều kiện để hai đường thẳng y = kx + b và y = k’x + b’ vuông góc với nhau.

5.(Để giải Bài toán 3)
Viết tọa độ hai vectơ chỉ phương:

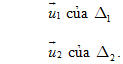
Hãy chứng tỏ rằng

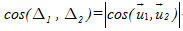
Từ đó đi đến các kết quả sau đây

6. Tìm góc giữa hai đường thẳng

trong mỗi trường hợp sau:

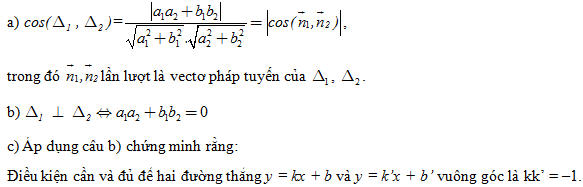
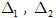
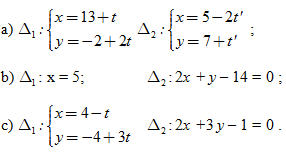
Câu hỏi và bài tập
15. Trong các mệnh đề sau, mệnh đề nào đúng?
a) Côsin của góc giữa hai đường thẳng a và b bằng côsin của góc giữa hai vectơ chỉ phương của chúng.
b) Nếu hai đường thẳng

và

lần lượt có phương trình px + y + m = 0 và x + py + n = 0 thì

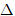
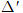
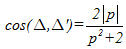
c) Trong tam giác ABC ta có

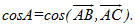
d) Nếu

là góc giữa hai đường thẳng chứa hai cạnh AB, AC của tam giác ABC thì

e) Hai điểm (7 ; 6) và (-1 ; 2) nằm về hai phía của đường thẳng y = x.

16. Cho ba điểm A(4 ; -1), B(-3 ; 2), C(1 ; 6). Tính góc BAC và góc giữa hai đường thẳng AB, AC.

17. Viết phương trình đường thẳng song song và cách đường thẳng ax + by + c = 0 một khoảng bằng h cho trước.

18. Cho ba điểm A(3 ; 0), B(-5 ; 4) và P(10 ; 2). Viết phương trình đường thẳng đi qua P đồng thời cách đều A và B.

19. Cho điểm M(2 ; 3). Viết phương trình đường thẳng cắt hai trục tọa độ ở A và B sao cho ABM là tam giác vuông cân tại đỉnh M.

20. Cho hai đường thẳng

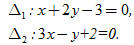
Viết phương trình đường thẳng đi qua điểm P(3 ; 1) và cắt

lần lượt ở A, B sao cho

tạo với

một tam giác cân có cạnh đáy là AB.


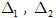
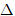
SƯU TẦM