Bài 3: Logarit.

[HuyNam]

Bài 3: Logarit.


<font size="4"><strong><span style="color:#0000ff;">

Với a là một số dương khác 1 và b là một số dương, số thực α thỏa mãn a[SUP]α[/SUP] = b được gọi là lôgarit cơ số a của b và kí hiệu

.
Lôgarit của tích hai số bằng tổng của lôgarit hai số đó:

Nhờ quy tắc này mà nhiều thế kỷ trước các nhà toán học và kỹ thuật có thể sử dụng bảng lôgarit để thực hiện phép nhân hai số thông qua phép cộng lôgarit, do phép cộng thì dễ tính hơn phép nhân. Nhà toán học John Napier đã phát minh ra phép tính này ở thế kỷ 17.
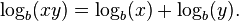
Để sử dụng bảng lôgarit, người ta thường đưa về lôgarit cơ số a = 10, gọi là lôgarit thập phân để thuận tiện cho tra bảng và tính toán.Lôgarit tự nhiên lấy hằng số e (xấp xỉ bằng 2,718) làm cơ số, và nó được sử dụng rộng rãi trong toán thuần túy. Lôgarit nhị phân với cơ số bằng 2 được sử dụng trong khoa học máy tính.
Thang lôgarit cho phép thu hẹp các đại lượng về phạm vi nhỏ hơn. Ví dụ, độ Richter đo năng lượng của động đất cũng sử dụng thang đo lôgarit, decibel là đơn vị lôgarit đo áp suất âm thanh. Lôgarit cũng thường gặp trong các công thức khoa học và kỹ thuật, như đo độ phức tạp của thuật toán và fractal, thậm chí trong công thức đếm số nguyên tố.