-
Chào mừng Bạn tham gia Diễn Đàn VNKienThuc.com - Định hướng Forum Kiến Thức - HÃY TẠO CHỦ ĐỀ KIẾN THỨC HỮU ÍCH VÀ CÙNG NHAU THẢO LUẬN Kết nối: VNK X - VNK groups | Nhà Tài Trợ: BhnongFood X - Bhnong groups - Đặt mua Bánh Bhnong
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Đấu trường hình không gian đây
- Thread starter son93
- Ngày gửi
NHÀ TÀI TRỢ
-
KBH Nong Food - Bánh gạo lứt, thực phẩm dinh dưỡng hàng đầu ăn sáng
- Latest: Khoa 22222222 444444r
Mình trình bày cách của mình nhé!
Các của Hương là 1 cách nhưng hơi phức tạp phải vẽ bảng thiên.
dễ thấy \[\alpha \leq \frac{\Pi }{2}\]
vì thế sin và cos đó dương.
cần tìm max của \[A = sin^2\alpha cos\alpha\]
\[A^2 = (sin^2\alpha )^2.cos^2\alpha = \frac{1}{2}.sin^2\alpha .sin^2\alpha (2-2sin^2\alpha )\]
áp dụng cosy cho biểu thức trên
\[A^2\leq \frac{(2-2sin^2\alpha +sin^2\alpha+sin^2\alpha)^3}{2.27}=\frac{4}{27}\]
dấu bằng sảy ra khi \[sin\alpha =\sqrt{\frac{2}{3}}\]
thỏa mãn!
done!
Các của Hương là 1 cách nhưng hơi phức tạp phải vẽ bảng thiên.
dễ thấy \[\alpha \leq \frac{\Pi }{2}\]
vì thế sin và cos đó dương.
cần tìm max của \[A = sin^2\alpha cos\alpha\]
\[A^2 = (sin^2\alpha )^2.cos^2\alpha = \frac{1}{2}.sin^2\alpha .sin^2\alpha (2-2sin^2\alpha )\]
áp dụng cosy cho biểu thức trên
\[A^2\leq \frac{(2-2sin^2\alpha +sin^2\alpha+sin^2\alpha)^3}{2.27}=\frac{4}{27}\]
dấu bằng sảy ra khi \[sin\alpha =\sqrt{\frac{2}{3}}\]
thỏa mãn!
done!
nhân tiện các bạn đang làm về tìm thiết diên j mình ra bài này(chủ yếu để rèn luyện kĩ năng tìm thiết diện thôi,không khó gì cả)
cho hình chóp S.ABCD,đáy là hình thang(AB//CD).M,N,P thuộc lần lượt SA,SB,SC.
a/tìm thiết diện đi qua M,N,P
b/tìm thiết diện đi qua M, // (SBC)
c/tìm thiết diện đi qua M, song song SD và BC
d/tìm thiết diện đi qua M,N,//BC;thiết diện đi qua M,P,//BC
(giả thiết đáy là hình thang có thể bỏ và phải xét nhiều trường hợp hơn.đề bài tự ra thôi,nhưng mình thấy có thể rèn luyện được phần xác định thiết diện với quan hệ song song)
cho hình chóp S.ABCD,đáy là hình thang(AB//CD).M,N,P thuộc lần lượt SA,SB,SC.
a/tìm thiết diện đi qua M,N,P
b/tìm thiết diện đi qua M, // (SBC)
c/tìm thiết diện đi qua M, song song SD và BC
d/tìm thiết diện đi qua M,N,//BC;thiết diện đi qua M,P,//BC
(giả thiết đáy là hình thang có thể bỏ và phải xét nhiều trường hợp hơn.đề bài tự ra thôi,nhưng mình thấy có thể rèn luyện được phần xác định thiết diện với quan hệ song song)
Tiếp tục topic này nhé!
Sơn ra đòn này, phản đòn đi:
Cho tứ diện gần đều ABCD trong đó AB = CD = a, BC = AD = b, AC = BD = c. Tính khoảng cách tứ các đỉnh của tứ diện tới các mặt đối diện.
Mời các bạn tiếp tục tham gia đấu trường, Sơn sẵn lòng "tiếp chiêu" các bạn (trong khuôn khổ kiến thức thi đại học, đừng thách đố nhé!)
Sơn ra đòn này, phản đòn đi:
Cho tứ diện gần đều ABCD trong đó AB = CD = a, BC = AD = b, AC = BD = c. Tính khoảng cách tứ các đỉnh của tứ diện tới các mặt đối diện.
Mời các bạn tiếp tục tham gia đấu trường, Sơn sẵn lòng "tiếp chiêu" các bạn (trong khuôn khổ kiến thức thi đại học, đừng thách đố nhé!)
Cảm ơn bản, nhưng hình như sai rồi! mình hỏi khoảng cách màminh` ra dien tich la`. đúng không vậy?
Mình làm bài này nhé, nhưng chỉ nêu cách giải thôi nhé:
Trước tiên dựng thiết diện như sau:
EF cắt các đường A'D' và A'B' lần lượt tại M và N. AM cắt D'D tại P, AN cắt BB' tại Q, thiết diện cần tìm là APFEQ. có nhiều cách tính thể tích, mình trình bày cách của mình, mình sẽ tính thể tích của tứ diện vuông D'.PMF (tính đơn giản) và tứ diện B'.ENQ (bẳng thể tích tứ diện D'.PMF) rồi tính thể tích tứ diện AA'MN, trừ đi thể tích của 2 tứ diện kia là xong!
cảm ơn bạn đã gửi bài về, rất vui được trao đổi kiến thức cùng bạn, mời bạn suy nghĩ bài của mình trên nhé!
Trước tiên dựng thiết diện như sau:
EF cắt các đường A'D' và A'B' lần lượt tại M và N. AM cắt D'D tại P, AN cắt BB' tại Q, thiết diện cần tìm là APFEQ. có nhiều cách tính thể tích, mình trình bày cách của mình, mình sẽ tính thể tích của tứ diện vuông D'.PMF (tính đơn giản) và tứ diện B'.ENQ (bẳng thể tích tứ diện D'.PMF) rồi tính thể tích tứ diện AA'MN, trừ đi thể tích của 2 tứ diện kia là xong!
cảm ơn bạn đã gửi bài về, rất vui được trao đổi kiến thức cùng bạn, mời bạn suy nghĩ bài của mình trên nhé!
hi .đúng ùi đó.bạn có vẻ rất thích và giỏi hình không gian nhỉ .mình gửi bạn bài khác he.
Cho lăng trụ tam giác đều ABCA'B'C' ,cạnh đáy a. đường chéo BC' của mặt bên BCC'B' tạo với mặt bên ABB'A' 1 góc
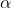 .C/minh thể tích khối lăng trụ là V=
.C/minh thể tích khối lăng trụ là V=
 .tìm
.tìm
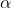 để lăng trụ tồn tại.
để lăng trụ tồn tại.
ak` cái đáp số diện tích là mình trả lời 1 cái bài nào trước đo âsk' chứ không phải của bài tính khoảng cách
Cho lăng trụ tam giác đều ABCA'B'C' ,cạnh đáy a. đường chéo BC' của mặt bên BCC'B' tạo với mặt bên ABB'A' 1 góc
ak` cái đáp số diện tích là mình trả lời 1 cái bài nào trước đo âsk' chứ không phải của bài tính khoảng cách
mình chỉ nêu cách giải thôi nhéhi .đúng ùi đó.bạn có vẻ rất thích và giỏi hình không gian nhỉ .mình gửi bạn bài khác he.
Cho lăng trụ tam giác đều ABCA'B'C' ,cạnh đáy a. đường chéo BC' của mặt bên BCC'B' tạo với mặt bên ABB'A' 1 góc.C/minh thể tích khối lăng trụ là V=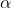 .tìm
.tìm để lăng trụ tồn tại.
để lăng trụ tồn tại.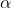
ak` cái đáp số diện tích là mình trả lời 1 cái bài nào trước đo âsk' chứ không phải của bài tính khoảng cách
M là trung điểm của A'B' vậy suy ra C'M vuông góc với mp(AA'B'B) góc giữa BC' là góc C'BM từ. hơn nữa BM vuông góc với C'M nên tính được BC' theo a, lại có tam giác BB'C vuông tại B' (lăng trụ đều) sau đó tính được BB' (đường cao của lăng trụ) thế là tính được thể tích rồi!hi
còn đk của góc đã cho là nhọn!
(không đúng thì góp ý nhé)
Thân!
Tiếp tục topic này nhé!
Sơn ra đòn này, phản đòn đi:
Cho tứ diện gần đều ABCD trong đó AB = CD = a, BC = AD = b, AC = BD = c. Tính khoảng cách tứ các đỉnh của tứ diện tới các mặt đối diện.
Mời các bạn tiếp tục tham gia đấu trường, Sơn sẵn lòng "tiếp chiêu" các bạn (trong khuôn khổ kiến thức thi đại học, đừng thách đố nhé!)
ek sơn.kết quả khoảng cách có phải là
Cách này mình thấy dài dòng quá mà nếu không biết công thức tính V liên hệ vs những đường vuông góc chung thì chịu. bạn có cách nào ngắn hơn thì chỉ mình nhá.
Gọi M,N,P,Q,R,S lần lượt là trung điểm AB,CD,AC,BD,AD,BC .thì MN,PQ,RS là những đoạn vuông góc chung . mình chứng minh được công thức thể tích
 = 1/3 .MN.PQ.RS .theo đl đường trung tuyến áp dụng vào tam giác BCN :
= 1/3 .MN.PQ.RS .theo đl đường trung tuyến áp dụng vào tam giác BCN :
 ( không biết mình nhớ nhầm không nữa).tính được BN rui` tính được MN .mấy cái kia tương tự. thế vào tính được V
( không biết mình nhớ nhầm không nữa).tính được BN rui` tính được MN .mấy cái kia tương tự. thế vào tính được V
Mà
 = 1/3 d(a, (BCD)).
= 1/3 d(a, (BCD)).
 .tính được diện tích tam giác BCD theo công thức S=
.tính được diện tích tam giác BCD theo công thức S=
 vs p là nửa chu vi tam giác. Sau đó cho 2 cái V đó bằng nhau rồi rút ra khoảng cách. Đúng không vậy?.hi
vs p là nửa chu vi tam giác. Sau đó cho 2 cái V đó bằng nhau rồi rút ra khoảng cách. Đúng không vậy?.hi
Gọi M,N,P,Q,R,S lần lượt là trung điểm AB,CD,AC,BD,AD,BC .thì MN,PQ,RS là những đoạn vuông góc chung . mình chứng minh được công thức thể tích
Mà
Sơn làm nhacho tứ diện ABCD có AB=AC=a, BC=b .hai mặt phẳng (BCD)và (ABC) vuông góc với nhau và góc BDC =90 độ >Xác định tâm và tính bán kính mặt câu ngoại tiếp ABCD theo a,b.
mọi người làm nha!
M là trung điểm của BC suy ra AM là trung trực của BC, N là trung điểm của CD, vậy (AMC) vuông góc với CD, tâm mặt cầu cần tìm là tâm đường tròn ngoại tiếp tam giác ABC. Bán kính bạn tự tính nha
Bài đó mình gợi ý nha bạn vẽ hình ra...(thế!) dựng tiếp trên (BCD) các đường thẳng qua C song song với BD, qua B song song với CD, qua D song song với BC, cắt nhau tại M, N, P. Nhận xét được tứ điện A.MNP vuông tại A, tính các cạnh của tứ diện trên là xong!Cách này mình thấy dài dòng quá mà nếu không biết công thức tính V liên hệ vs những đường vuông góc chung thì chịu. bạn có cách nào ngắn hơn thì chỉ mình nhá.
Gọi M,N,P,Q,R,S lần lượt là trung điểm AB,CD,AC,BD,AD,BC .thì MN,PQ,RS là những đoạn vuông góc chung . mình chứng minh được công thức thể tích= 1/3 .MN.PQ.RS .theo đl đường trung tuyến áp dụng vào tam giác BCN : ( không biết mình nhớ nhầm không nữa).tính được BN rui` tính được MN .mấy cái kia tương tự. thế vào tính được V
( không biết mình nhớ nhầm không nữa).tính được BN rui` tính được MN .mấy cái kia tương tự. thế vào tính được V
Mà= 1/3 d(a, (BCD)). .tính được diện tích tam giác BCD theo công thức S=
.tính được diện tích tam giác BCD theo công thức S= vs p là nửa chu vi tam giác. Sau đó cho 2 cái V đó bằng nhau rồi rút ra khoảng cách. Đúng không vậy?.hi
vs p là nửa chu vi tam giác. Sau đó cho 2 cái V đó bằng nhau rồi rút ra khoảng cách. Đúng không vậy?.hi
dễ thấy tam giác ABS vuông tại S, tính được đường cao của tam giác đó cũng chính là đường cao của khối chóp đường cao đó có độ lớn:Cho hình chóp SABCD có đáy ABCD là hình vuông cạnh 2a,SA=a ,SB=và mp(SAD) vuông góc vs mặt phẳng đáy.Gọi M,N lần lượt là trung điểm AB,BC.Tính theo a thể tích của khối chóp SBMDN.TÍnh cosin của góc giữa 2 đường thẳng SM,DN.
Sơn cũng post vài bài lên làm cho zui đi.
\[\frac{a^2\sqrt{3}}{2a}=\frac{a\sqrt{3}}{2}\]
diện tích của tứ giác BMDN \[2a^2\] vậy thể tích của khối chóp
\[\frac{a^3}{\sqrt{3}}\]
Bài của mình à?! Đây nè:
Cho lăng trụ \[ABC.A'B'C'\] có độ dài cạnh bên là \[2a\], đáy là tam giác vuông tại A có\[ AB = a\], \[AC =a\sqrt{3}\]. Hình chiếu vuông góc của đỉnh A' lên \[(ABC)\] là trung điểm của BC. Tính góc giữa 2 đường thẳng AA' và B'C'. Hãy tính thể tích của lăng trụ theo a./
Cho lăng trụ \[ABC.A'B'C'\] có độ dài cạnh bên là \[2a\], đáy là tam giác vuông tại A có\[ AB = a\], \[AC =a\sqrt{3}\]. Hình chiếu vuông góc của đỉnh A' lên \[(ABC)\] là trung điểm của BC. Tính góc giữa 2 đường thẳng AA' và B'C'. Hãy tính thể tích của lăng trụ theo a./
Xếp Hạng
-
9,009
Butchi
-
5,105
Hide Nguyễn
-
4,376
ButNghien
-
4,163
Thandieu2
-
2,603
Trang Dimple
-
2,579
ngan trang
-
2,213
Văn Sử Địa
-
2,069
ButBi
-
1,872
Nguyễn Thành Sáng
-
1,766
h2y3
Tương tác
-
-
-
Thông Báo Máy Lạnh Âm Trần Toshiba – Giải Pháp Làm Mát Thẩm Mỹ & Hiệu Quả
- Latest: tinhtrieuan
-
-
-
NHÀ TÀI TRỢ
-
KBH Nong Food - Bánh gạo lứt, thực phẩm dinh dưỡng hàng đầu ăn sáng
- Latest: Khoa 22222222 444444r
Chủ đề mới
-
Thông Báo Máy lạnh âm trần Samsung – Mát sâu, tiết kiệm điện vượt trội
- Started by tinhtrieuan
- Trả lời: 0
-
Thông Báo Máy Lạnh Âm Trần AQA Giải Pháp Lý Tưởng Cho Không Gian Mở
- Started by tinhtrieuan
- Trả lời: 0
-
Thông Báo Máy Lạnh Âm Trần Toshiba – Giải Pháp Làm Mát Thẩm Mỹ & Hiệu Quả
- Started by tinhtrieuan
- Trả lời: 0
-
Thông Báo Máy Lạnh Âm Trần Toshiba Inverter – Vận Hành Êm, Bền Bỉ
- Started by tinhtrieuan
- Trả lời: 0
-
Thông Báo Máy Lạnh Âm Trần LG Cho Không Gian Lớn | Hiệu Suất Vượt Trội
- Started by tinhtrieuan
- Trả lời: 0
Dành cho học sinh
-
Mọi người ơi, cho mình hỏi hsg 9 cần học nlvh những dạng nào vậy?
- Started by Peter X
- Trả lời: 1
-
Bước qua ranh giới an toàn của bản thân có thực sự đáng sợ?"
- Started by Bút Nghiên
- Trả lời: 0
-
-
-
-
-
-
-
Điểm chuẩn là gì? Điểm sàn là gì? Điểm chuẩn đánh giá năng lực là gì?
- Started by VN Kiến Thức
- Trả lời: 5
-
Các chứng chỉ tiếng Anh thông dụng tại Việt Nam hiện nay
- Started by Sugilite
- Trả lời: 4
Trending content
-
-
S
-
-
Định hướng
Diễn đàn VnKienthuc.com là nơi thảo luận và chia sẻ về mọi kiến thức hữu ích trong học tập và cuộc sống, khởi nghiệp, kinh doanh,...
