Hình 11_Nâng cao _Chương II_Bài 3. Đường thẳng song song với mặt phẳng
1. Vị trí tương đối giữa đường thẳng và mặt phẳng
Cho một đường thẳng a và một mặt phẳng (P). Ta thấy có ba trường hợp sau đây xảy ra:
a) Đường thẳng a và mp(P) có hai điểm chung phân biệt. Khi đó, theo định lí ở §1, đường thẳng a nằm trên mp(P), tức là
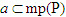

b) Đường thẳng a và mp(P) có một điểm chung duy nhất A. Khi đó ta nói a và (P) cắt nhau tại A và viết
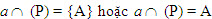
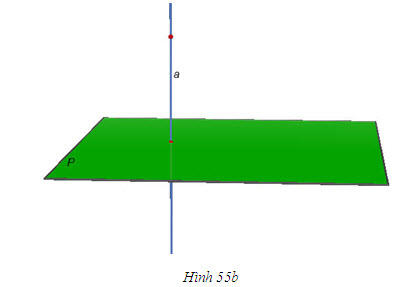
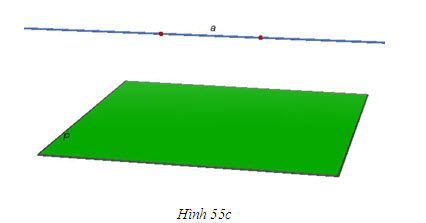
c) Đường thẳng a và mp(P) không có điểm chung nào cả. Khi đó ta nói rằng đường thẳng a song song với mặt phẳng (P), hoặc mặt phẳng(P) song song với đường thẳng a, hoặc a và (P) song song với nhau, và viết a // (P) hoặc (P) // a (h.55c).
Vậy ta có định nghĩa sau đây
ĐỊNH NGHĨA
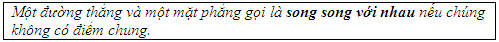
2. Điều kiện để một đường thẳng song song với một mặt phẳng
Nhận xét
Cho đường thẳng b nằm trong mp(P) và một đường thẳng a song song với b. Lấy một điểm I tùy ý trên a. Khi đó, nếu I thuộc (P) thì a nằm trong (P); nếu I không thuộc (P) thì a song song với (P) (h.56).
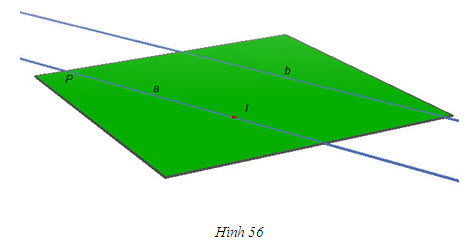
Vậy ta có định lí sau đây
ĐỊNH LÍ 1

3. Tính chất
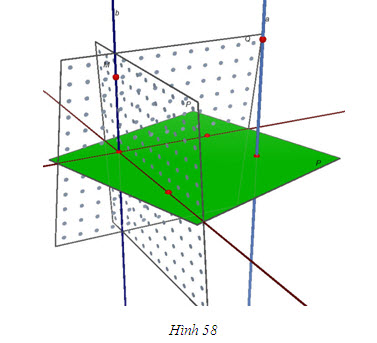
Cho đường thẳng a song song với mặt phẳng (P). Khi đó, đường thẳng a có song song với đường thẳng nào nằm trên (P) hay không? Định lí sau đây giúp ta thấy rõ điều đó.
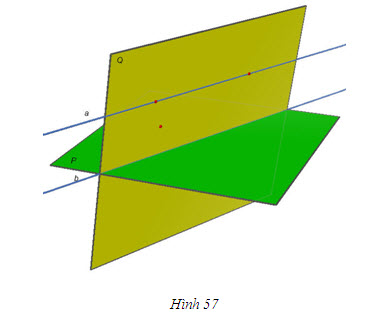
ĐỊNH LÍ 2


Hãy vẽ qua a một mặt phẳng (Q) cắt mặt phẳng (P) theo giao tuyến b rồi dùng phương pháp phản chứng để chứng minh b song song với a(h.57).
HỆ QUẢ 1
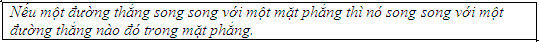
HỆ QUẢ 2


Cho hai mặt phẳng (P), (Q) cùng song song với một đường thẳng a và
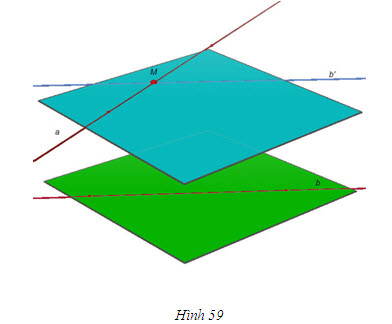
ĐỊNH LÍ 3
Chứng minh
Lấy một điểm M nằm trên a. Kẻ qua M một đường thẳng b’ song song với b (h.59). Khi đó, theo định lí 1, hai đường thẳng a và b’ xác định mp(P) song song với b.
Nếu có mặt phẳng (Q) khác (P) cũng đi qua a và song song với b thì theo hệ quả 2, a là giao tuyến của (P) và (Q) nên a // b , trái với giả thiết. Vậy mp(P) là duy nhất.
Ví dụ
Cho tứ diện ABCD. Gọi M là một điểm nằm trên cạnh AB (M khác A và B). Giả sử (P) là mặt phẳng qua M song song với các đường thẳng AC và BD. Hãy xác định thiết diện của hình tứ diện ABCD khi cắt bởi mặt phẳng (P). Thiết diện là hình gì ?
Giải(h.60)
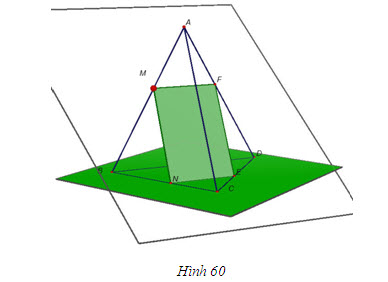
Từ M kẻ đường thẳng song song với AC cắt BC tại N và kẻ đường thẳng song song với BD cắt AD tại F. Khi ấy, (P) chính là mp(MNF). Gọi E là giao điểm của (P) với CD thì thiết diện là tứ giác MNEF. Vì đường thẳng MN song song với mp(ACD) nên mp(P) qua MN cắt mp(ACD) theo giao tuyến EF song song với MN. Tương tự, NE song song với MF. Vậy thiết diện cần tìm là hình bình hành MNEF.
Câu hỏi và bài tập
23. Cho hai đường thẳng a và b cùng song song với mp(P). Mệnh đề nào đúng trong các mệnh đề sau ?a) a và b song song với nhau;
b) a và b chéo nhau;
c) a và b có thể cắt nhau;
d) a và b trùng nhau;
e) Các mệnh đề a), b), c), d) đều sai.
24. Cho mp(P) và hai đường thẳng song song a, b. Mệnh đề nào đúng trong các mệnh đề sau đây?
a) Nếu (P) song song với a thì (P) cũng song song với b;
b) Nếu (P) song song với athì (P) song song với b hoặc chứa b;
c) Nếu (P) song song với a thì (P) chứa b;
d) Nếu (P) cắt a thì (P) cũng cắt b;
e) Nếu (P) cắt a thì (P) có thể song song với b;
f) Nếu (P) chứa a thì (P) có thể song song với b.
25. Cho hình tứ diện ABCD. Gọi M, N lần lượt là trung điểm của các cạnh AB và AC.
a) Xét vị trí tương đối của đường thẳng MN và mp(BCD).
b) Gọi d là giao tuyến của hai mặt phẳng (DMN) và (DBC). Xét vị trí tương đối của d và mp(ABC).
26. Khi cắt tứ diện bằng một mặt phẳng thì thiết diện nhận được có thể là những hình nào sau đây?
a) Hình thang;
b) Hình bình hành;
c) Hình thoi.
27. Cho hình chóp S.ABCD có đáy là tứ giác lồi. O là giao điểm của hai đường chéo AC và BD. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng đi qua O, song song với AB và SC. Thiết diện đó là hình gì?
28. Cho hình chóp S.ABCD có đáy là hình bình hành. Xác định thiết diện của hình chóp khi cắt bởi mặt phẳng đi qua trung điểm M của cạnh AB, song song với BD và SA.
SƯU TẦM
